Question

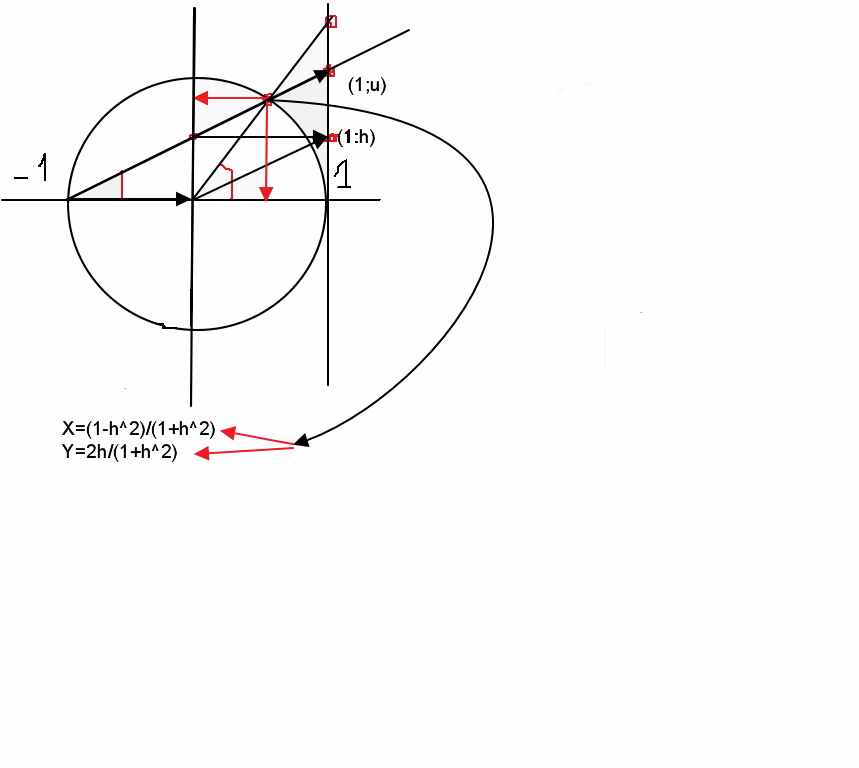
Помогите не совсем понятно снизу формулы сверху графическая интерпритация , как получили из верхнего те формулы снизу ?

Answer 1

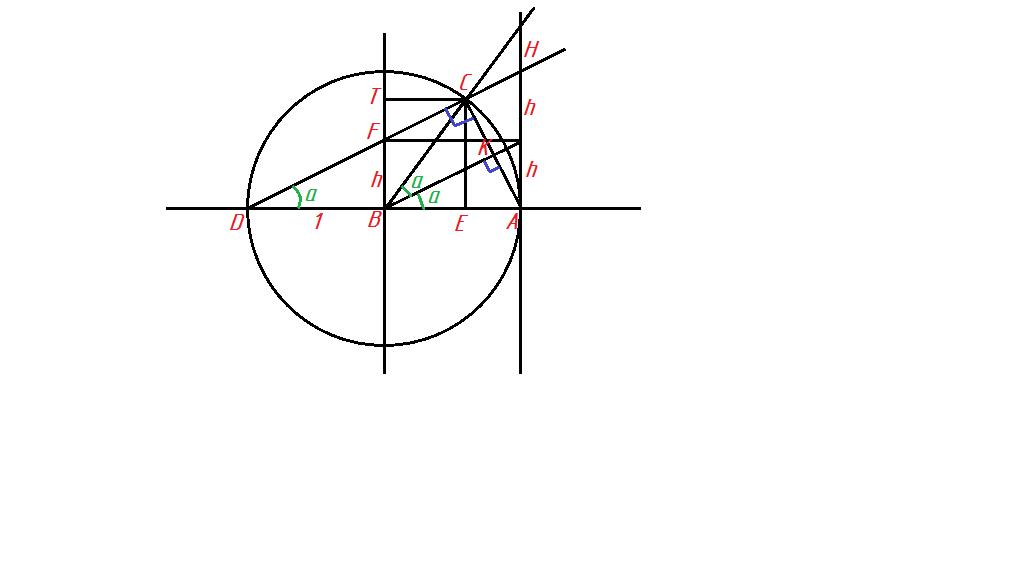
Сделаем дополнительные построения как показано на рисунке во вложении.
Заметим далее, что треугольник DBF подобен треугольнику DAH, коэффициент подобия равен двум.
Найдем тангенс угла HDA:
$tga = frac{2h}{2}=h$
Найдем далее синус и косинус того же угла применяя тождества:
$1+tg^2a=frac{1}{cos^2a}$
$1+ctg^2a=frac{1}{sin^2a}$
Получаем:
$cos a=sqrt{frac{1}{1+h^2}}$
$sin a=hsqrt{frac{1}{1+h^2}}$
Угол HDA является вписанным в окружность, а значит равен половине центрального угла CBA, что отмечено на рисунке.
Треугольник СВК равен треугольнику КВА, по трем сторонам.
В треугольнике ВКА, найдем КА:
$sin a = frac{KA}{1}$
$KA= sin a = hsqrt{frac{1}{1+h^2}}$
Так как СК=КА(радиус перпендикулярен хорде) получаем:
$CA= 2KA=2hsqrt{frac{1}{1+h^2}}$
Рассмотрим далее треугольник DCA, найдем сторону CD:
$tga=frac{CA}{CD}$
$CD=frac{CA}{tga}=frac{2h}{h}cdotsqrt{frac{1}{1+h^2}}=2sqrt{frac{1}{1+h^2}}$
Исходя из треугольника CDE найдем найдем сторону CE:
$sin a = frac{CE}{CD}$
$CE = CDsin a = 2sqrt{frac{1}{1+h^2}}cdot hsqrt{frac{1}{1+h^2}}=frac{2h}{1+h^2}$
Здесь CE является координатой по оси Оу, тогда длина отрезка СТ будет равна координате по оси Ох.
Рассмотрим прямоугольник СТВЕ, зная что СВ=ВА=1(из равенства треугольников) находим длину отрезка ВЕ, используя теорему Пифагора:
$EB^2=sqrt{CB^2-CE^2}=sqrt{1-left(frac{2h}{1+h^2}right)^2}=sqrt{frac{(1+h^2)^2 -(2h)^2}{(1+h^2)^2}}=frac{1-h^2}{1+h^2}$
Получаем координаты точки:
$left(frac{2h}{1+h^2};frac{1-h^2}{1+h^2}right)$
Которые вынесены вниз.