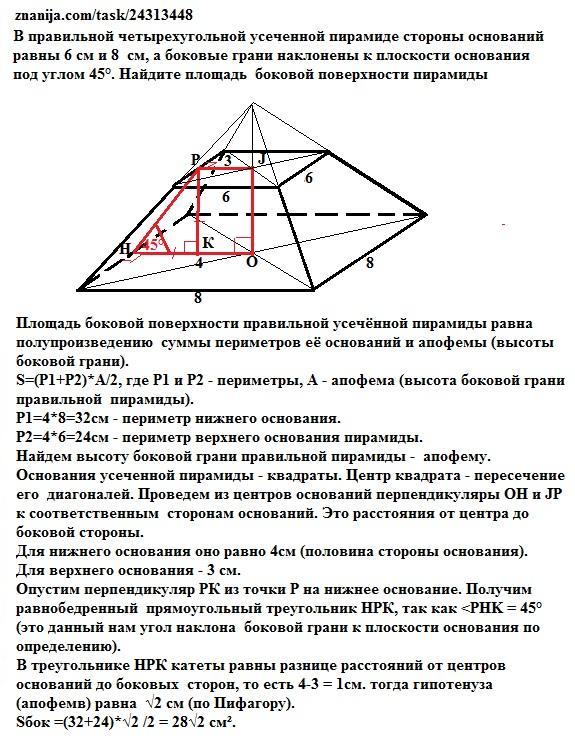
В правильной четырехугольной усеченной пирамиде стороны оснований равны 6 см и 8 см, а боковые грани наклонены к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды
Ответы
Площадь боковой поверхности правильной усечённой пирамиды равна половине произведения суммы периметров её оснований и апофемы (высоты боковой грани).
S=(Р1+Р2)*А/2, где Р1 и Р2 - периметры, А - апофема (высота боковой грани правильной пирамиды)
Р1=4*8=32см - периметр нижнего основания.
Р2=4*6=24см - периметр верхнего основания пирамиды.
Найдем высоту боковой грани правильной пирамиды - апофему.
Основания усеченной пирамиды - квадраты. Центр квадрата - пересечение его диагоналей. Проведем из центров оснований перпендикуляры ОН и JP к соответственным сторонам оснований. Это расстояния от центра до боковой стороны.
Для нижнего основания оно равно 4см (половина стороны основания). Для верхнего основания - 3 см.
Опустим перпендикуляр РК из точки Р верхнего основания на нижнее основание. Получим равнобедренный прямоугольный треугольник НРК, так как <PHK = 45° (это данный нам угол наклона боковой грани к плоскости основания по определению).
В треугольнике НРК катеты равны разнице расстояний от центров оснований до боковых сторон, то есть 4-3 = 1см. тогда гипотенуза (апофемв) равна √2 см (по Пифагору).
Sбок =(32+24)*√2 /2 = 28√2 см².