Предмет: Геометрия,
автор: марьямка25
В правильном четырехугольной пирамиде плоский угол при вершине равен альфа .Найдите объем пирамиды если ее высота равна h
Ответы
Автор ответа:
0
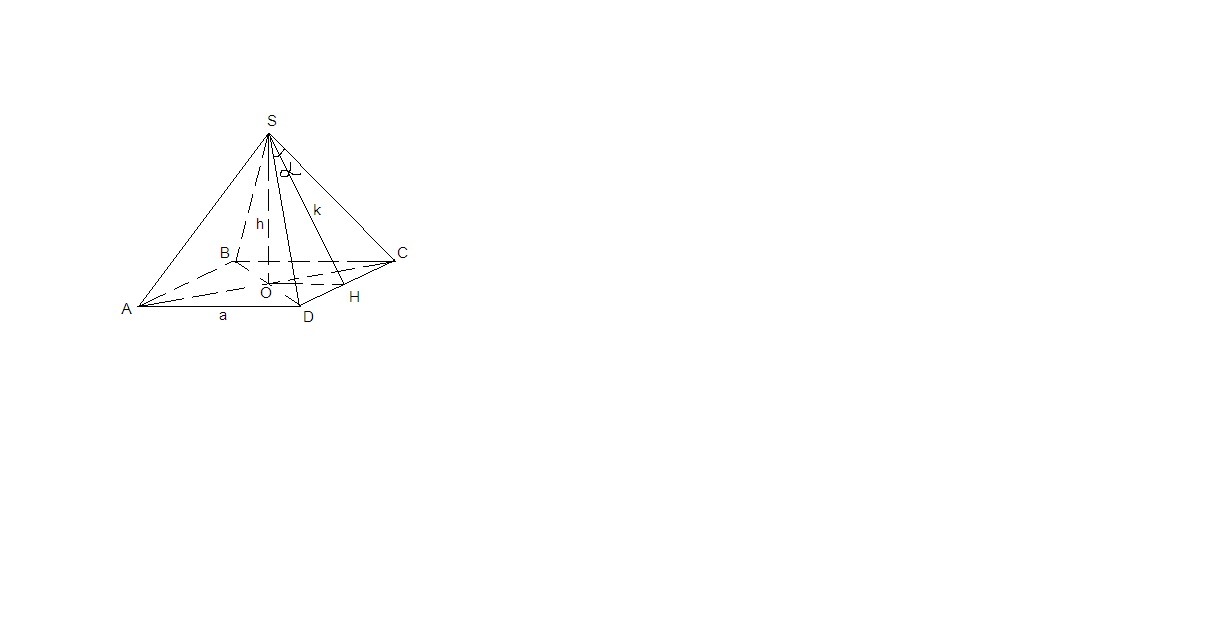
Пусть H - середина CD.
CH = a/2, ∠CSH = α/2
ΔCSH: ∠H = 90°
tg(α/2) = (a/2)/k
a/2 = k·tg(α/2)
OH = AD/2 = a/2 (средняя линия ΔACD)
ΔSOH: ∠O=90°
(a/2)² = k² - h² по теореме Пифагора
a/2 = k·tg(α/2)
(a/2)² = k² - h²
(a/2)² = k² ·tg²(α/2)
(a/2)² = k² - h²
k² ·tg²(α/2) = k² - h²
k² - k² ·tg²(α/2) = h²
k²(1 - tg²(α/2)) = h²
k² = h² / (1 - tg²(α/2))
a² = 4k² - 4h²
a² = 4h² / (1 - tg²(α/2)) - 4h² =
= 4h²(1/ (1 - tg²(α/2)) - 1) = 4h²((1 - 1 + tg²(α/2))/ (1 - tg²(α/2)) =
= 4h²(tg²(α/2) )/ (1 - tg²(α/2)) - это площадь основания
V = 1/3 Sосн·h = 1/3 · 4h² · tg²(α/2) / (1 - tg²(α/2)) · h =
= 4h³ · tg²(α/2)/ (3(1 - tg²(α/2)))
CH = a/2, ∠CSH = α/2
ΔCSH: ∠H = 90°
tg(α/2) = (a/2)/k
a/2 = k·tg(α/2)
OH = AD/2 = a/2 (средняя линия ΔACD)
ΔSOH: ∠O=90°
(a/2)² = k² - h² по теореме Пифагора
a/2 = k·tg(α/2)
(a/2)² = k² - h²
(a/2)² = k² ·tg²(α/2)
(a/2)² = k² - h²
k² ·tg²(α/2) = k² - h²
k² - k² ·tg²(α/2) = h²
k²(1 - tg²(α/2)) = h²
k² = h² / (1 - tg²(α/2))
a² = 4k² - 4h²
a² = 4h² / (1 - tg²(α/2)) - 4h² =
= 4h²(1/ (1 - tg²(α/2)) - 1) = 4h²((1 - 1 + tg²(α/2))/ (1 - tg²(α/2)) =
= 4h²(tg²(α/2) )/ (1 - tg²(α/2)) - это площадь основания
V = 1/3 Sосн·h = 1/3 · 4h² · tg²(α/2) / (1 - tg²(α/2)) · h =
= 4h³ · tg²(α/2)/ (3(1 - tg²(α/2)))
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: alinababek
Предмет: Обществознание,
автор: yulka0105
Предмет: Математика,
автор: алена2ващугина
Предмет: Музыка,
автор: barrvera