Предмет: Геометрия,
автор: sasadaskevic8031
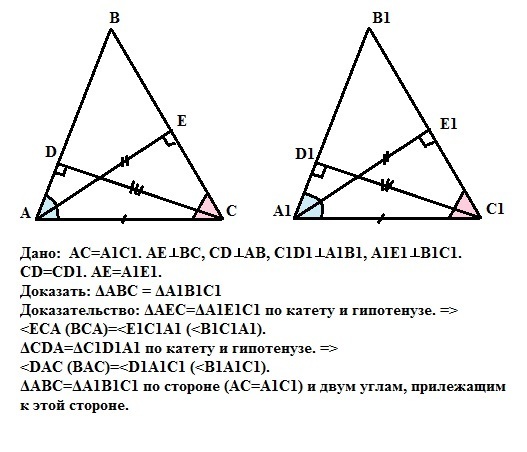
Докажите,что два остроугольных треугольника равны,если сторона и высоты, проведенные из концов этой стороны,одного треугольника соответственно равны стороне и высотам, проведенным из концов этой стороны,другого треугольника.
Ответы
Автор ответа:
0
Пусть даны треугольники АВС и А1В1С1, у которых стороны АС и А1С1 равны. Высоты, проведенные из концов этих сторон к боковым сторонам треугольников, также равны. То есть АЕ = А1Е1 и СD = C1D1. Прямоугольные треугольники АЕС и А1Е1С1, ADC и A1D1C1 равны по катету и гипотенузе (четвертый признак равенства прямоугольных треугольников) так как АС=А1С1 (гипотенуза), а АЕ=А1Е1 и CD=C1D1 (катеты) - дано.Из этого равенства следует равенство углов DAC и D1A1C1, а также углов АСЕ И А1С1Е1. Тогда треугольники АВС и А1В1С1 равны по второму признаку равенства треугольников, так как у них равны стороны (АС=А1С1) и углы, прилежащие к этим сторонам (<ВАС = <В1А1С1 и <ВСА=<В1А1С1 - доказано выше).
Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: brawlakk888p
Предмет: Математика,
автор: begamega2010
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: ежик342
Предмет: Литература,
автор: lyubasmi2009