Предмет: Геометрия,
автор: nicegoroshko1
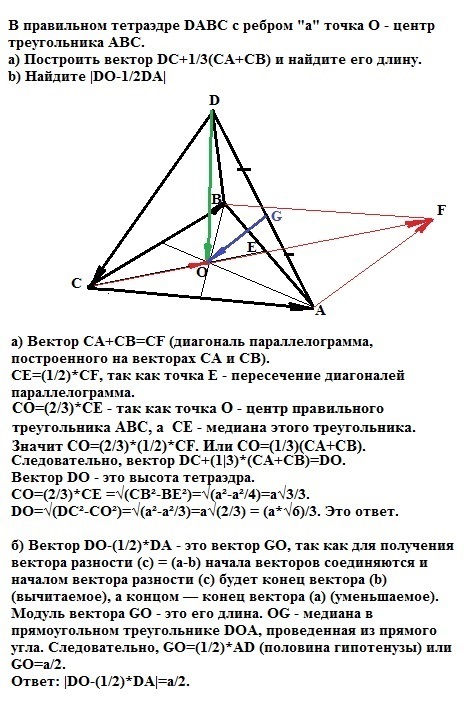
2) В правильном тетраэдре DABC с ребром a точка О - центр треугольника ABC. a) Построить вектор DC+1/3(CA+CB) и найдите его длину. b) Найдите |DO-1/2DA|
Ответы
Автор ответа:
0
а) Вектор СА+СВ=СF (диагональ параллелограмма, построенного на векторах СА и СВ).
CЕ=(1/2)*СF, так как точка Е - пересечение диагоналей параллелограмма.
СО=(2/3)*СЕ - так как точка О - центр правильного треугольника АВС, а
СЕ - медиана этого треугольника.
Значит СО=(2/3)*(1/2)*СF. Или СО=(1/3)(СА+СВ).
Следовательно, вектор DC+(1/3)*(CA+CB)=DO.
Вектор DO - это высота тетраэдра.
СО=(2/3)*СЕ =√(CВ²-ВЕ²)=√(a²-a²/4)=a√3/3.
DO=√(DC²-CO²)=√(a²-a²/3)=a√(2/3) = (a*√6)/3. Это ответ.
б) Вектор DO-(1/2)*DA - это вектор GO, так как для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Модуль вектора GO - это его длина. ОG - медиана в прямоугольном треугольнике DOA, проведенная из прямого угла. Следовательно, GO=(1/2)*AD (половина гипотенузы) или GO=a/2.
Ответ: |DO-(1/2)*DA|=a/2.
CЕ=(1/2)*СF, так как точка Е - пересечение диагоналей параллелограмма.
СО=(2/3)*СЕ - так как точка О - центр правильного треугольника АВС, а
СЕ - медиана этого треугольника.
Значит СО=(2/3)*(1/2)*СF. Или СО=(1/3)(СА+СВ).
Следовательно, вектор DC+(1/3)*(CA+CB)=DO.
Вектор DO - это высота тетраэдра.
СО=(2/3)*СЕ =√(CВ²-ВЕ²)=√(a²-a²/4)=a√3/3.
DO=√(DC²-CO²)=√(a²-a²/3)=a√(2/3) = (a*√6)/3. Это ответ.
б) Вектор DO-(1/2)*DA - это вектор GO, так как для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Модуль вектора GO - это его длина. ОG - медиана в прямоугольном треугольнике DOA, проведенная из прямого угла. Следовательно, GO=(1/2)*AD (половина гипотенузы) или GO=a/2.
Ответ: |DO-(1/2)*DA|=a/2.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: dzangazievbrejnli
Предмет: Биология,
автор: wjhd
Предмет: Русский язык,
автор: tenmariya0059
Предмет: Литература,
автор: untdragon