Предмет: Геометрия,
автор: ВладEagle
Задача. Найдите косинус угла между плоскостями ромба  и равностороннего треугольника
и равностороннего треугольника  , если
, если  см, ∠
см, ∠  ° и расстояние от точки
° и расстояние от точки  до прямой
до прямой  равно
равно  см. (с рисунком!)
см. (с рисунком!)
Ответы
Автор ответа:
0
а=АД=8 см. ∠α=∠ВАД=30°.
Для начала найдём высоту ромба.
S(АВСД)=а²·sinα=8²/2=32 см².
S(АВСД)=a·Н ⇒ Н=S(АВСД)/а=32/8=4 см.
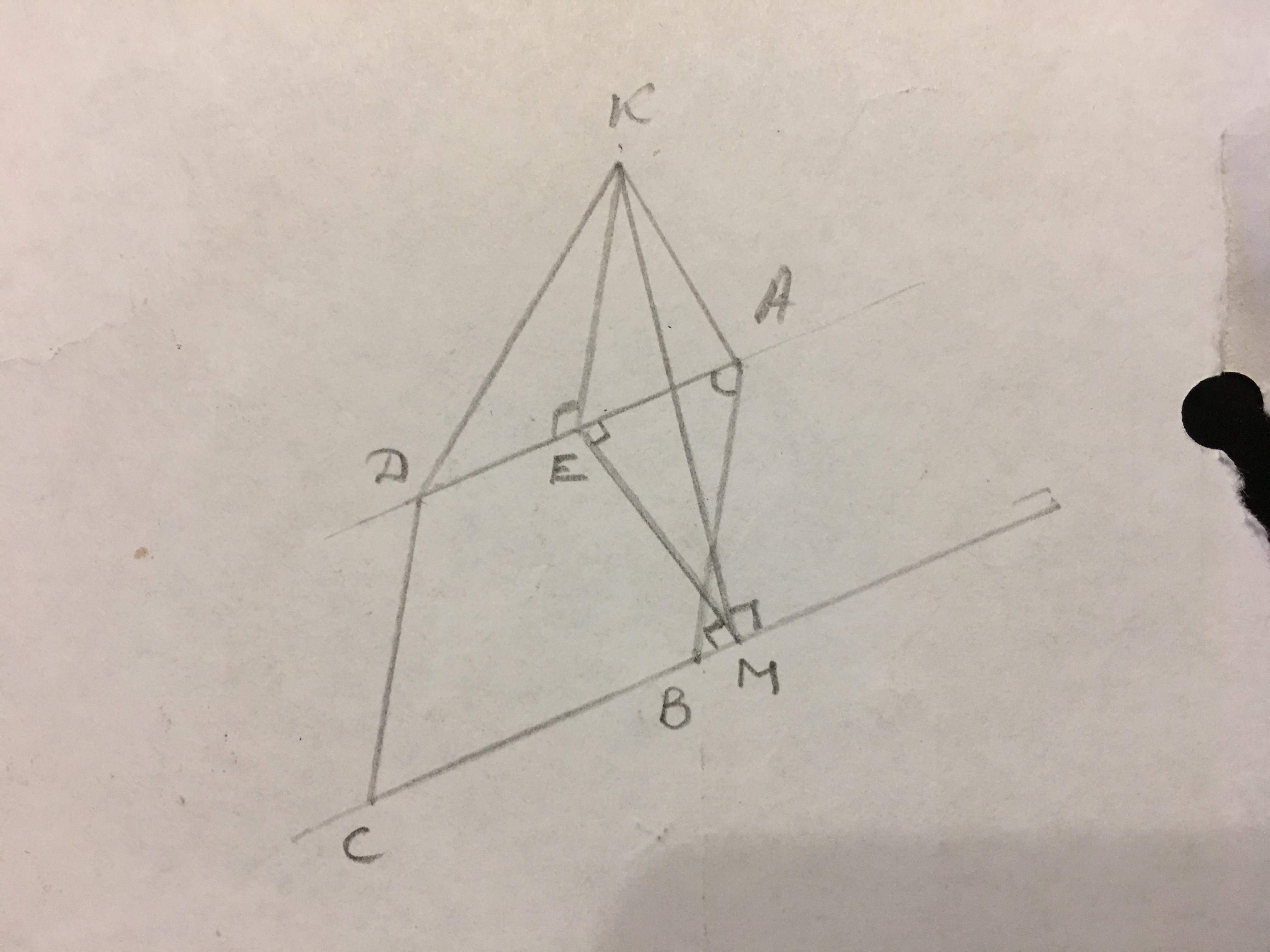
В правильном треугольнике АДК КЕ - высота. КЕ=а√3/2=4√3 см.
Прямые АД и ВС параллельны. Проведём МЕ⊥АД, М∈ВС ⇒ МЕ⊥ВС. МЕ=Н=4 см.
КЕ⊥АД и МЕ⊥ВС, значит по теореме о трёх перпендикулярах КМ⊥ВС, следовательно КМ=4√2 см (по условию).
КЕ⊥АД и МЕ⊥АД, значит ∠КЕМ - линейный угол двугранного угла КАДМ или угол между плоскостями АДК и АВС.
В треугольнике КМЕ по теореме косинусов:
cos∠КЕМ=(КЕ²+МЕ²-КМ²)/(2КЕ·МЕ),
cos∠КЕМ=(48+16-32)/(2·4√3·4)=32/(32√3)=1/√3 - это ответ.
Для начала найдём высоту ромба.
S(АВСД)=а²·sinα=8²/2=32 см².
S(АВСД)=a·Н ⇒ Н=S(АВСД)/а=32/8=4 см.
В правильном треугольнике АДК КЕ - высота. КЕ=а√3/2=4√3 см.
Прямые АД и ВС параллельны. Проведём МЕ⊥АД, М∈ВС ⇒ МЕ⊥ВС. МЕ=Н=4 см.
КЕ⊥АД и МЕ⊥ВС, значит по теореме о трёх перпендикулярах КМ⊥ВС, следовательно КМ=4√2 см (по условию).
КЕ⊥АД и МЕ⊥АД, значит ∠КЕМ - линейный угол двугранного угла КАДМ или угол между плоскостями АДК и АВС.
В треугольнике КМЕ по теореме косинусов:
cos∠КЕМ=(КЕ²+МЕ²-КМ²)/(2КЕ·МЕ),
cos∠КЕМ=(48+16-32)/(2·4√3·4)=32/(32√3)=1/√3 - это ответ.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: kardenis75
Предмет: Математика,
автор: dashkachikareva
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: алина1101
Предмет: Математика,
автор: Дурдом1