Question

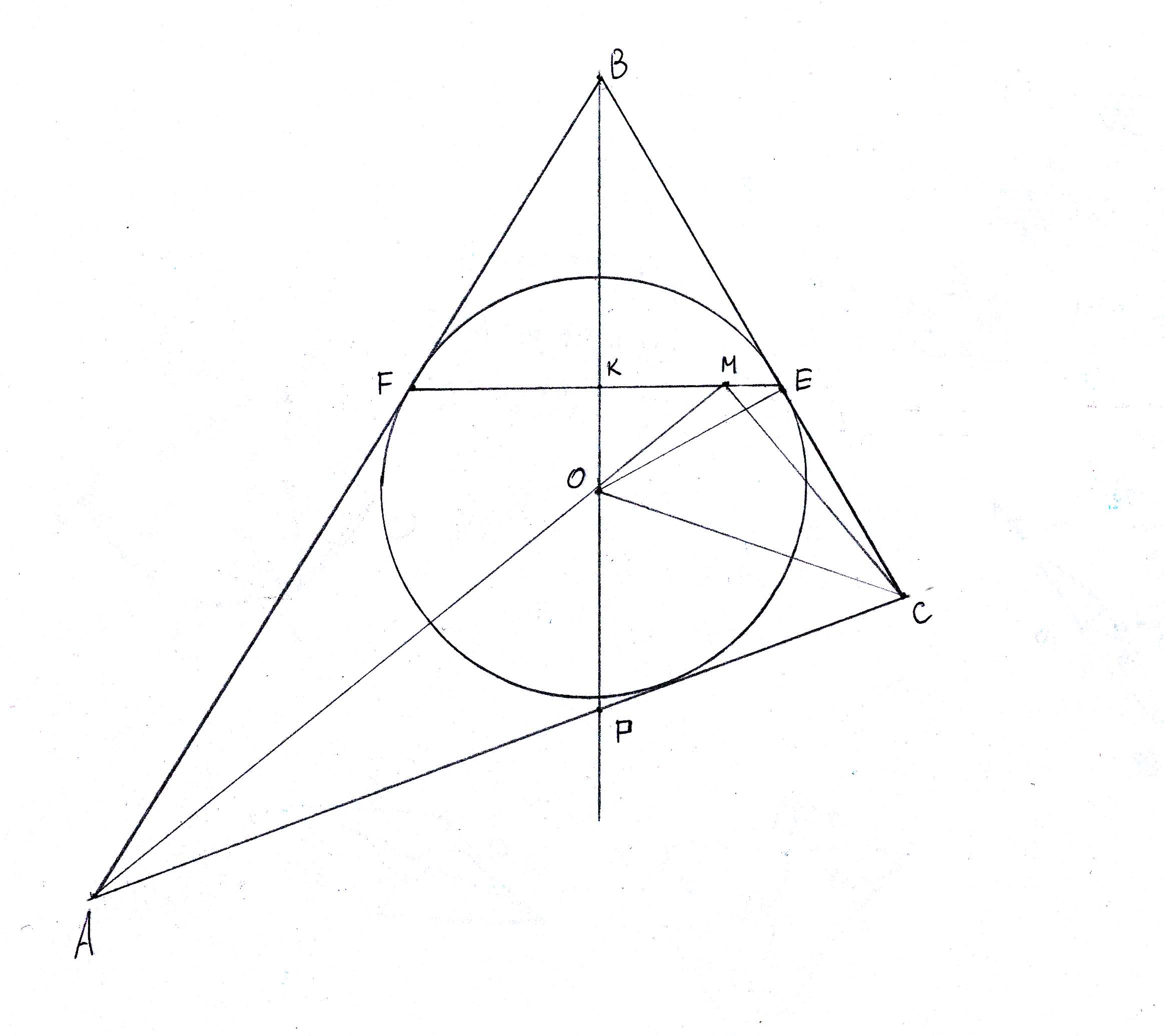
В треугольнике ABC вписанная окружность касается сторон BC и BA в точках E и F. М - точка пересечения биссектрисы угла А с прямой EF. Найти величину AMC.

Answer 1

См. чертеж. Ясно, что АО, ВО и СО - биссектрисы.
Угол MOC - внешний угол треугольника AOC,
поэтому угол MOC = A/2 + C/2;  (А, B и С - углы треугольника ABC);
Треугольник BKE прямоугольный, так как BO перпендикулярна FE. 
Угол KEC - внешний угол треугольника BKE, 
поэтому угол KEC = 90° + B/2;
получилось, что угол MOC + угол KEC = A/2 + C/2 + B/2 + 90° = 180°;
Это означает, что вокруг четырехугольника OMEC можно описать окружность.
В этой окружности углы OMC и OEC вписанные и опирающиеся на одну дугу, поэтому они равны, и - поскольку угол OEC = 90°, то угол OMC тоже равен 90°; (а OC - диаметр этой окружности).