Предмет: Математика,
автор: maria4290
вычислить двойной интеграл по области d (cos2x+siny)dxdy ограничены х=0 у=0 4x+4y-pi=0
Ответы
Автор ответа:
0
Приложения:
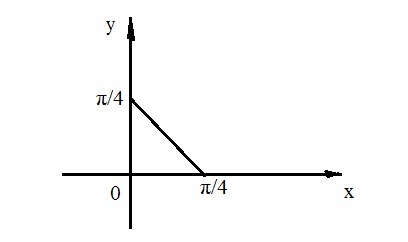
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: nikish228xg
Предмет: Алгебра,
автор: irinali8210
Предмет: Химия,
автор: SgtRamenator
Предмет: Математика,
автор: Isaevanastya1