Question

Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведена прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5

Answer 1

Ответ: R=5 (ед. длины)

Объяснение:  

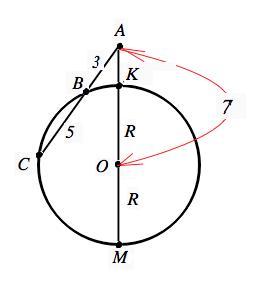
      Пусть точка пересечения окружности с отрезком АО  - К, а с ее продолжением - М (см. рисунок приложения).

АС и АМ - секущие.

По теореме о двух секущих:

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на её внешнюю часть: ⇒

                   АС•АВ=АМ•АК

АС=АВ+ВС=3+5=8

АМ=АО+ОМ=7+R

AK=AO-R=7-R  ⇒

8•3=(7-R)•(7+R)  

24=7²-R² ⇒

R²=49-24=25 ⇒

R=√25=5 (ед. длины)