Предмет: Геометрия,
автор: ололо18
Найти площадь равнобедренного треугольника, если основание его равно "а", а длина высоты, проведенной к основанию равна длине отрезка, соединяющего середины основания и боковой стороны.
Ответы
Автор ответа:
0
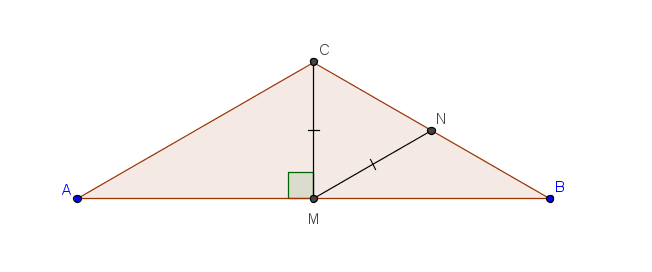
MN - средняя линия треугольника ABC, AC = 2MN = 2CM;
Треугольник ACM - прямоугольный, гипотенуза AC в 2 раза больше катета CM, тогда угол А равен 30 градусов.
CM = AM / tg A = AM / sqrt(3) = a / 2 / sqrt(3) = a sqrt(3) / 6
S(ABC) = 1/2 CM * AB = a^2 sqrt(3) / 12
Треугольник ACM - прямоугольный, гипотенуза AC в 2 раза больше катета CM, тогда угол А равен 30 градусов.
CM = AM / tg A = AM / sqrt(3) = a / 2 / sqrt(3) = a sqrt(3) / 6
S(ABC) = 1/2 CM * AB = a^2 sqrt(3) / 12
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: nikolaskorik
Предмет: История,
автор: bajmurzinasamala
Предмет: Алгебра,
автор: pavlosemencuk996
Предмет: Алгебра,
автор: pff