Предмет: Алгебра,
автор: divone68
Помогите пожалуйста решить. cosx=(cosx/2 - sin x/2 ) в квадрате -1
Приложения:
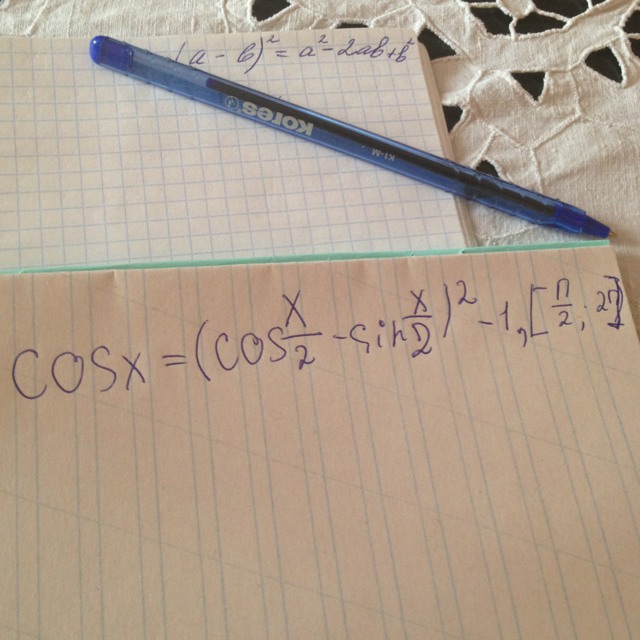
Ответы
Автор ответа:
0
cosx = (cosx/2 - sinx/2)^2 - 1
cosx = cos^2 x/2 - 2sinx/2cosx/2 + sin^2 x/2 - 1 cos^2 x/2 + sin^2 x/2 = 1
cosx = 1 - sin(2*x/2) - 1
cosx = -sinx Раделим обе части уравнения на sinx не = 0
сtgx = -1
x = -pi/4 + pin
Ответ. -pi/4 + pin, где n принадлежит Z
cosx = cos^2 x/2 - 2sinx/2cosx/2 + sin^2 x/2 - 1 cos^2 x/2 + sin^2 x/2 = 1
cosx = 1 - sin(2*x/2) - 1
cosx = -sinx Раделим обе части уравнения на sinx не = 0
сtgx = -1
x = -pi/4 + pin
Ответ. -pi/4 + pin, где n принадлежит Z
Похожие вопросы
Предмет: Физика,
автор: rabotnik105060
Предмет: Русский язык,
автор: emilbalasultanov1
Предмет: Русский язык,
автор: lyna8365
Предмет: Литература,
автор: AlexFiona