Предмет: Математика,
автор: mel9977
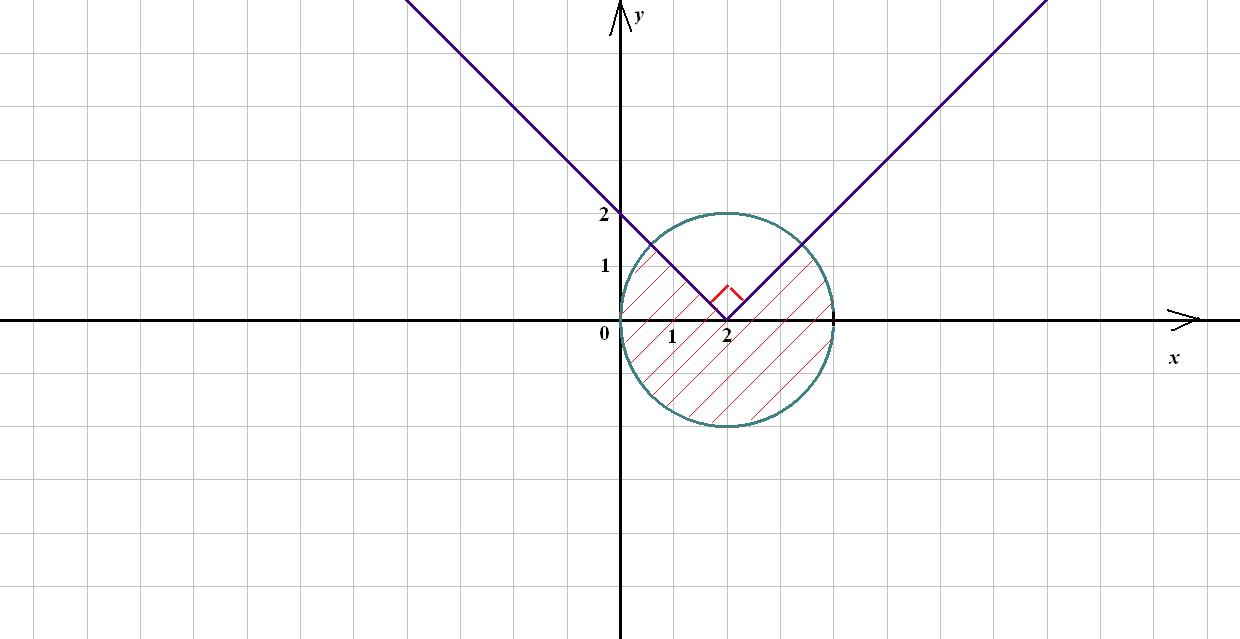
найти площадь фигуры, которая задана неравенством x^2+y^2<4x и y</x-2/
Ответы
Автор ответа:
0
Рисунок во вложении.
Искомая площадь заштрихована. Ее площадь равна
Приложения:
Похожие вопросы
Предмет: Химия,
автор: danilkakalina
Предмет: Русский язык,
автор: emilbalasultanov1
Предмет: Геометрия,
автор: soficoblack
Предмет: Алгебра,
автор: propapopa
Предмет: Математика,
автор: алинчик345