Предмет: Алгебра,
автор: Аноним
Вычислите.......................................
Приложения:
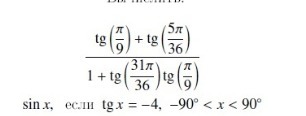
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: lavrovaola25
Предмет: Геометрия,
автор: stadnik20376
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: 4143
Предмет: Литература,
автор: panda7979