Question

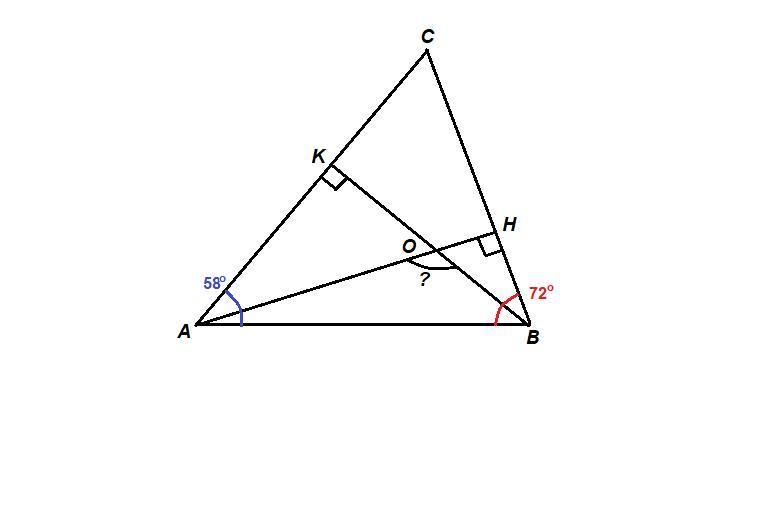
Два угла треугольника равны 58° и 72°. Найдите тупой угол, который
образуют высоты треугольника, выходящие из вершин этих углов. Ответ
дайте в градусах. (2 способа решения)

Answer 1

Ответ:

    130°

Объяснение:

1 способ.

Сумма острых углов прямоугольного треугольника равна 90°.

ΔАНВ:  ∠ АНВ = 90°,

            ∠ВАН = 90° - ∠АВН = 90° - 72° = 18°

ΔВКА:  ∠ВКА = 90°,

            ∠АВК = 90° - ∠ВАК = 90° - 58° = 32°

ΔАОВ:  

∠АОВ = 180° - (∠ВАО + ∠АВО) = 180° - (18° + 32°) =

= 180° - 50° = 130°

2 способ.

Из ΔАВС:  

∠С = 180° - (∠А + ∠В) = 180° - (58° + 72°) = 180° - 130° = 50°

Сумма углов выпуклого четырехугольника равна 360°.

Для четырехугольника СКОН:

∠КОН = 360° - (∠С + ∠К + ∠Н) = 360° - (50° + 90° + 90°) =

= 360° - 230° = 130°