Question

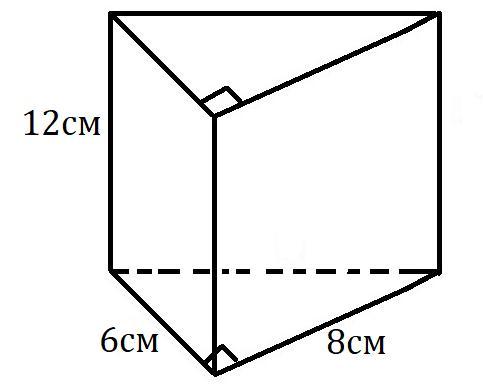
В прямой треугольной призме-прямоугольный треугольник с катетами 8 см и 6 см.Боковое ребро призмы равно 12см.Найдите площадь полной поверхности призмы.

Answer 1

найдем третью сторону основания, это гипотенуза, по теореме пифагора гипотенуза равна сумме квадратов катетов

с*с=8*8+6*6=100 кв.см, с =10 см

S1=2*(1/2)*8*6=48 кв.см - площадь оснований

S2=12*(8+6+10)=208 кв.см- площадь боковой поверхности

S=48+208=256 кв.см - площадь полной поверхности 

 

Answer 2

В прямой призме боковые грани это прямоугольники.

Найдём по теореме Пифагора гипотенузу прямоугольного треугольника из оснований.

$displaystyle sqrt{8^2 +6^2 } =2sqrt{4^2 +3^2 } =2sqrt{25} =2cdot 5=10$

Площадь одного основания найдём как площадь прямоугольного треугольника, через катеты:

$displaystyle frac12 cdot 8cdot 6 =4cdot 6=24$ см²

Тогда S(осн.) = 24·2 = 48см².

Площадь боковой поверхности найдём как сумму площадей прямоугольников:

S(бок.) = 12·6 + 12·8 + 12·10 = 12·(6+8+10) = (10+2)·24 = 240+48 = 288 см².

S(пол.) = S(осн.) + S(бок.) = 48+288 = 336 см².

Ответ: 336 см².