Предмет: Геометрия,
автор: lapinakatik
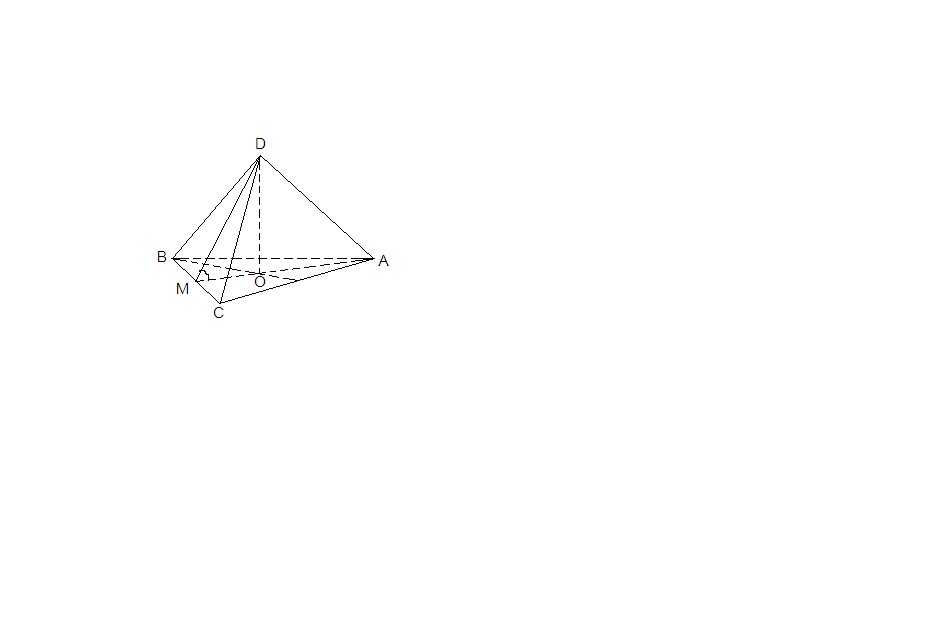
DABC - правильная треугольная пирамида. DO перпендикулярно ABC. АM перпендикулярно BC. AМ=9, угол DMO=30 градусов. Найти площадь боковой поверхности
Ответы
Автор ответа:
0
Основание высоты правильной пирамиды - центр ее основания. Значит, О - точка пересечения медиан (биссектрис и высот). ⇒ОМ = 1/3 АМ = 3 см.
ΔDMO: ∠O = 90°, cos∠M = OM / MD
√3/2 = 3/MD
MD = 6/√3 = 2√3 (см)
АМ - высота равностороннего треугольника, значит
АМ = BC√3/2
BC = 2AM/√3 = 18/√3 = 6√3 (см)
Sбок = 1/2 · Pосн · DM = 1/2 · 3BC · DM = 1/2 ·18√3 · 2√3 = 54 (см²)
ΔDMO: ∠O = 90°, cos∠M = OM / MD
√3/2 = 3/MD
MD = 6/√3 = 2√3 (см)
АМ - высота равностороннего треугольника, значит
АМ = BC√3/2
BC = 2AM/√3 = 18/√3 = 6√3 (см)
Sбок = 1/2 · Pосн · DM = 1/2 · 3BC · DM = 1/2 ·18√3 · 2√3 = 54 (см²)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gopicoyeahah
Предмет: Кыргыз тили,
автор: adelaasanbekova08120
Предмет: Математика,
автор: aruzanbajsadykova
Предмет: Математика,
автор: анна1013