Question

Помогите....Очнь надо..!
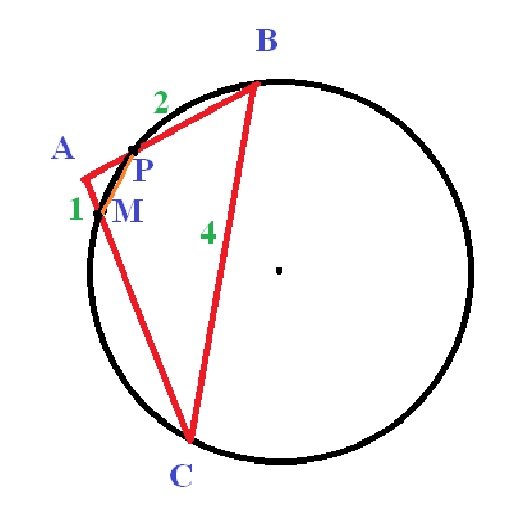
   В треугольнике АВС известны стороны АВ = 2, ВС = 4. Окружность,
проходящая через точки В и С, пересекает прямую АС в точке М, а прямую
АВ — в точке Р. Известно, что AM = 1. Найдите длину РМ.

Answer 1

Классная задача!!!
Чертеж во вложении.
По свойству секущих к окружности, проведенных из одной точки АМ*АС=АР*АВ.
Значит, можно составить отношение (опираясь на основное св-во пропорции):
$frac{AP}{AC}=frac{AM}{AB}=frac{1}{2}$
Отсюда тут же следует подобие треугольников АРМ и АВС по второму признаку (∠А-общий, отношения образующих его сторон треугольников равны 1/2).
В свою очередь отсюда следует отношение
$frac{1}{2}=frac{PM}{BC} => frac{1}{2}=frac{PM}{4} => PM=2$
Ответ: 2.