Предмет: Алгебра,
автор: Аноним
Объясните, подробно, как решать кубические уравнения.
Ответы
Автор ответа:
0
Самый простой вариант разложение на множители

Может встретится формула куба суммы или разности


Целым корнем может быть делитель свободного члена

Удобен вариант применения схемы Горнера, схема на картинке, вместо х нужно подставлять предполагаемый корень и если окажется равным 0, то х - корень исходного уравнения.
окажется равным 0, то х - корень исходного уравнения.
Может встретится формула куба суммы или разности
Целым корнем может быть делитель свободного члена
Удобен вариант применения схемы Горнера, схема на картинке, вместо х нужно подставлять предполагаемый корень и если
Приложения:
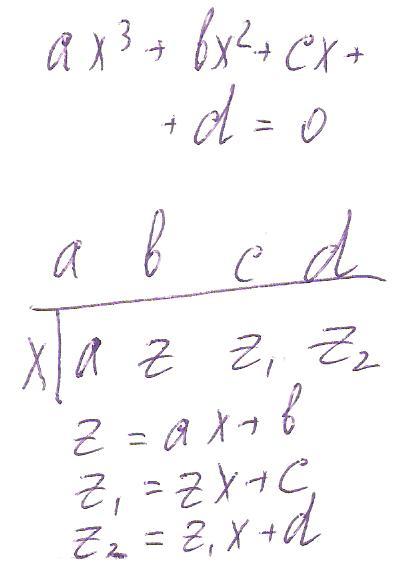
Автор ответа:
0
Можно, чуть подробней про схему Горнера?
Автор ответа:
0
Автор ответа:
0
Нам нужно узнать равно ли 0 число z2. Находим его через коэффициенты и предполагаемый корень по формулам, которые написаны на картинке. Если z2 не равно 0, то х - не корень, если z2=0, то x - корень + нам нужно решить уравнение ax^2+zx+z1=0 и если оно имеет корни, то они также будут являться корнями кубического уравнения
Автор ответа:
0
Спасибо
Похожие вопросы
Предмет: Химия,
автор: vika73nika
Предмет: Химия,
автор: Trofim101
Предмет: Литература,
автор: anutakurguz2620
Предмет: Биология,
автор: Наденькаа
Предмет: Алгебра,
автор: Paulina25