Предмет: Алгебра,
автор: WITCHDAGGAH
Алгебра 10 класс.
Прошу помочь, как можно скорее!
Приложения:
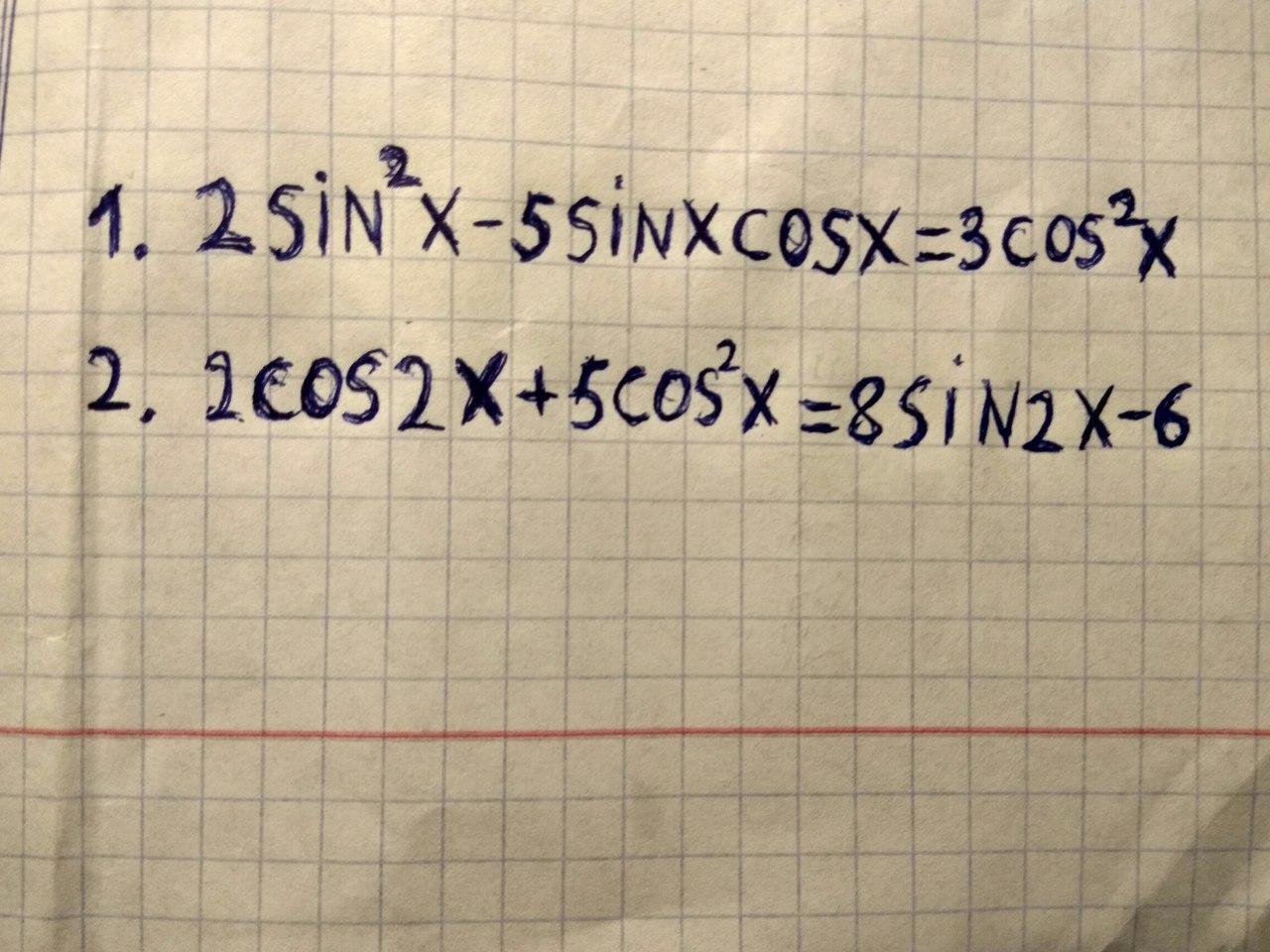
Ответы
Автор ответа:
0
1)Разделим обе части уравнения на cos²x:
2tg²x - 5tgx - 3 = 0
tgx = t
2t² - 5t - 3 = 0
D = 25 + 24 = 49
t = (5 - 7)/4= -1/2 или t = (5 + 7)/4 = 3
tgx = - 1/2 tgx = 3
x = - arctg 1/2 + πn x = arctg 3 + πk
2) Разложим по формуле косинус двойного угла и синус двойного угла. 6 в правой части умножим на "тригонометрическую единицу", на sin²x + cos²x
2cos²x - 2sin²x + 5cos²x - 16sinx·cosx + 6sin²x + 6cos²x = 0
4sin²x - 16sinx·cosx +13cos²x = 0
Делим на cos²x:
4tg²x - 16tgx + 13 = 0
tgx = t
4t² - 16t + 13 = 0
D/4 = 64 - 52 = 12
t = (8 + 2√3)/4 = (4 + √3)/2 или t = (8 - 2√3)/4 = (4 - √3)/2
tgx = (4 + √3)/2 tgx = (4 - √3)/2
x = arctg (4 + √3)/2 + πn x = arctg(4 - √3)/2 + πk
2tg²x - 5tgx - 3 = 0
tgx = t
2t² - 5t - 3 = 0
D = 25 + 24 = 49
t = (5 - 7)/4= -1/2 или t = (5 + 7)/4 = 3
tgx = - 1/2 tgx = 3
x = - arctg 1/2 + πn x = arctg 3 + πk
2) Разложим по формуле косинус двойного угла и синус двойного угла. 6 в правой части умножим на "тригонометрическую единицу", на sin²x + cos²x
2cos²x - 2sin²x + 5cos²x - 16sinx·cosx + 6sin²x + 6cos²x = 0
4sin²x - 16sinx·cosx +13cos²x = 0
Делим на cos²x:
4tg²x - 16tgx + 13 = 0
tgx = t
4t² - 16t + 13 = 0
D/4 = 64 - 52 = 12
t = (8 + 2√3)/4 = (4 + √3)/2 или t = (8 - 2√3)/4 = (4 - √3)/2
tgx = (4 + √3)/2 tgx = (4 - √3)/2
x = arctg (4 + √3)/2 + πn x = arctg(4 - √3)/2 + πk
Автор ответа:
0
1.
2sin²x - 5sin x·cos x = 3cos²x
Делим почленно на cos²x.
2tg²x - 5tg x = 3
Замена: tg x = t
2t² - 5t - 3 = 0
D = 25+ 24 = 49
t = 5-7 / 4 = -1/2
t = 5+7 / 4 = 3
tg x = -1/2
tg x = 3
x = -arc tg 1/2 + πn, n ∈ Z
x = arc tg 3 + πk, k ∈ Z
2.
2cos 2x + 5cos²x = 8sin 2x - 6
7cos²x - 2sin²x = 16sin x·cos x - 6sin²x - 6cos² x
4sin²x - 16sin x·cos x + 13cos²x = 0
Делим почленно на cos²x.
4tg²x - 16tg x + 13 = 0
Замена: tg x = t
4t² - 16t + 13 = 0
D= 16² - 16·13 = 16·3 = 48
t = 16-√48 / 16 = 1 - √3/4
t = 16+√48 / 16 = 1 + √3/4
tg x = 1 - √3/4
tg x = 1 + √3/4
x = arc tg (1 - √3/4) + πn, n ∈ Z
x = arc tg (1 + √3/4) + πk, k ∈ Z
2sin²x - 5sin x·cos x = 3cos²x
Делим почленно на cos²x.
2tg²x - 5tg x = 3
Замена: tg x = t
2t² - 5t - 3 = 0
D = 25+ 24 = 49
t = 5-7 / 4 = -1/2
t = 5+7 / 4 = 3
tg x = -1/2
tg x = 3
x = -arc tg 1/2 + πn, n ∈ Z
x = arc tg 3 + πk, k ∈ Z
2.
2cos 2x + 5cos²x = 8sin 2x - 6
7cos²x - 2sin²x = 16sin x·cos x - 6sin²x - 6cos² x
4sin²x - 16sin x·cos x + 13cos²x = 0
Делим почленно на cos²x.
4tg²x - 16tg x + 13 = 0
Замена: tg x = t
4t² - 16t + 13 = 0
D= 16² - 16·13 = 16·3 = 48
t = 16-√48 / 16 = 1 - √3/4
t = 16+√48 / 16 = 1 + √3/4
tg x = 1 - √3/4
tg x = 1 + √3/4
x = arc tg (1 - √3/4) + πn, n ∈ Z
x = arc tg (1 + √3/4) + πk, k ∈ Z
Похожие вопросы
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: harinaanastasia808
Предмет: Химия,
автор: albinalajk18
Предмет: Математика,
автор: mstatynas
Предмет: Математика,
автор: rozakurasheva