Предмет: Геометрия,
автор: Физик1997
Точка О - точка пересечения биссектрис треугольника АВС. Прямая ВО пересекает описанную около треугольника АВС окружность в точке S. Найти длину отрезка ОS, если АС=sqrt(3+sqrt3), угол В=30 градусов, угол С=45 градусов.
Ответы
Автор ответа:
0
Вписанный угол в 30°
опирается на хорду, равную радиусу, а вписанный угол в 45° - на хорду,
стягивающую дугу в 90°, т.е. равную стороне вписанного в окружность квадрата.
Поэтому, если обозначить АС = b = √(3 + √3), то радиус описанной около АВС окружности R
= b; а АВ = b*√2;
Более того, точка S делит дугу АС (равную 60°) пополам (ВО - биссектриса), поэтому хорда SB стягивает дугу 90° + 30° = 120°, то есть BS = b*√3;
Все это очень хорошо, но найти надо OS, а для этого надо найти положение центра вписанной окружности.
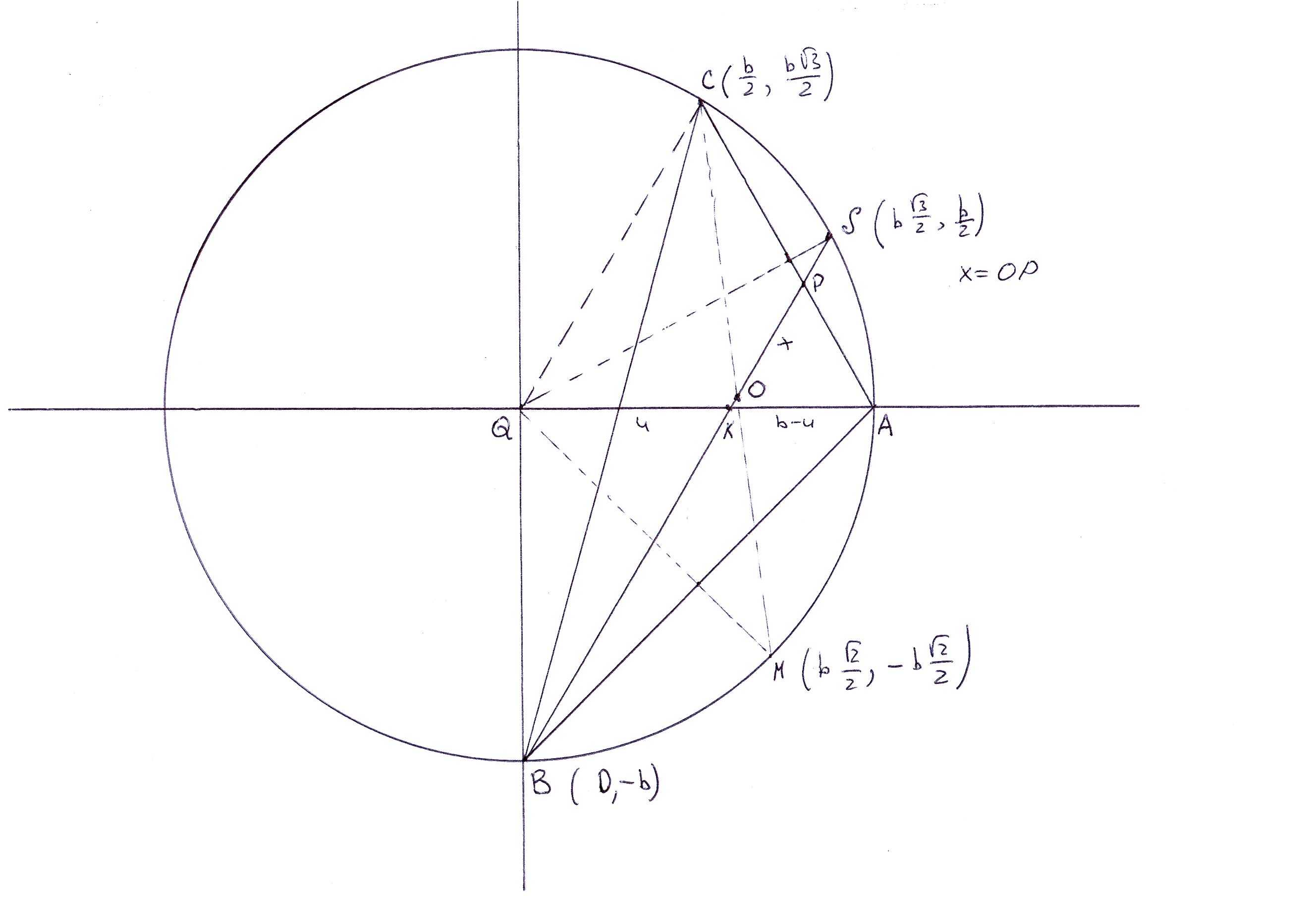
Если внимательно посмотреть на приложенный рисунок, то можно заметить несколько интересных особенностей этой конструкции. Если Q - центр описанной окружности, а К – точка пересечения QA и BS, то QC II BS (простым сравнением углов). Поскольку треугольник QAC равносторонний, то CP = QK, АР = КР = АК = b - QK; легко видеть, поскольку угол KBQ = 30°, что QK = b/√3; и ВК = 2*QK = b*2/√3; а BS = 3*QK (!).
Теперь надо вычислить и ВР, и ВО, и СВ. Для упрощения вычислений я введу несколько простых обозначений.
Пусть QK = u; ВС = a; AB = c; BP = μ – длина биссектрисы; y = BO; x = OP;
Тогда μ = BK + KP = 2*u + (b – u) = b + u; a/c = u/(b – u); a = c*u/(b – u);
По свойству биссектрисы y/x = (a + c)/b;
y/x = (c + c*u/(b – u))/b = c/(b – u); y + x = μ = b + u; y = c*(b + u)/(c + b – u);
Теперь сюда можно подставить значения u = b/√3; c = b*√2;
Получается BO = y = b*√2*(√3 + 1)/(√6 + √3 – 1);
OS = BS – BO = b*(√3 - √2*(√3 + 1)/(√6 + √3 – 1)) = √(3 + √3)*(√3 - √2*(√3 + 1)/(√6 + √3 – 1));
Я не буду искать упрощения этого выражения – подстановка в Excel и в Maple ничего не дала, так что это скорее всего бесполезно.
Ну, и хочется обратить внимание на то, что координатный метод тут просто сам просится - О это точка пересечения двух прямых СМ и BS, проходящих через точки с известными координатами, после определения координат точки О из соответствующей системы 2 линейных уравнений надо найти расстояние от O до S, координаты которой тоже известны.
Для любителей комплексных переменных - отдельно - координаты точки О вычисляются очень легко :)
Более того, точка S делит дугу АС (равную 60°) пополам (ВО - биссектриса), поэтому хорда SB стягивает дугу 90° + 30° = 120°, то есть BS = b*√3;
Все это очень хорошо, но найти надо OS, а для этого надо найти положение центра вписанной окружности.
Если внимательно посмотреть на приложенный рисунок, то можно заметить несколько интересных особенностей этой конструкции. Если Q - центр описанной окружности, а К – точка пересечения QA и BS, то QC II BS (простым сравнением углов). Поскольку треугольник QAC равносторонний, то CP = QK, АР = КР = АК = b - QK; легко видеть, поскольку угол KBQ = 30°, что QK = b/√3; и ВК = 2*QK = b*2/√3; а BS = 3*QK (!).
Теперь надо вычислить и ВР, и ВО, и СВ. Для упрощения вычислений я введу несколько простых обозначений.
Пусть QK = u; ВС = a; AB = c; BP = μ – длина биссектрисы; y = BO; x = OP;
Тогда μ = BK + KP = 2*u + (b – u) = b + u; a/c = u/(b – u); a = c*u/(b – u);
По свойству биссектрисы y/x = (a + c)/b;
y/x = (c + c*u/(b – u))/b = c/(b – u); y + x = μ = b + u; y = c*(b + u)/(c + b – u);
Теперь сюда можно подставить значения u = b/√3; c = b*√2;
Получается BO = y = b*√2*(√3 + 1)/(√6 + √3 – 1);
OS = BS – BO = b*(√3 - √2*(√3 + 1)/(√6 + √3 – 1)) = √(3 + √3)*(√3 - √2*(√3 + 1)/(√6 + √3 – 1));
Я не буду искать упрощения этого выражения – подстановка в Excel и в Maple ничего не дала, так что это скорее всего бесполезно.
Ну, и хочется обратить внимание на то, что координатный метод тут просто сам просится - О это точка пересечения двух прямых СМ и BS, проходящих через точки с известными координатами, после определения координат точки О из соответствующей системы 2 линейных уравнений надо найти расстояние от O до S, координаты которой тоже известны.
Для любителей комплексных переменных - отдельно - координаты точки О вычисляются очень легко :)
Приложения:
Автор ответа:
0
А что за химия теперь с очками? Мне баллы не нужны, но это же главная составляющая сервера, если тут обман, то чему верить? Вот за эту задачу обещано 10 баллов, дано 5 (так мне сообщил сервер). Кроме того, при добавлении решения мне заявляется, что я не могу решить задачу дважды. Это вообще бред - решать я могу хоть 100 раз, а добавлять больше одного решения - уж мне это точно в голову не придет.
Автор ответа:
0
Если так дальше будет продолжаться - я вернусь к тому, как делал когда то вначале - начну размещать решения только в комментариях. Мне же лучше - не надо удовлетворять глупые претензии халявщиков, если таковые появляются.
Автор ответа:
0
спасибо большое, помогли) и хорошо ваше решение оформили) еще раз-благодарю)
Автор ответа:
0
странное условие. обычно числа подбираются так, чтобы конечный ответ был выражен каким-то целым числом или как-то так... в данном случае я долго крутил числа, но похоже, составители промашку дали, или я так и не нашел... хотя само решение логически точное.
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: География,
автор: daniilshabanov793
Предмет: Геометрия,
автор: Alinkachechet
Предмет: Обществознание,
автор: Levacheva
Предмет: Алгебра,
автор: МарусЕЕЕчка