Question

В
четырехугольнике АВСD диагонали
пересекаются в точке О. Известно, что
АО — медиана треугольника ВАD, а ВО —
медиана треугольника АВС. Докажи, что
АВСD — параллелограмм.

Answer 1

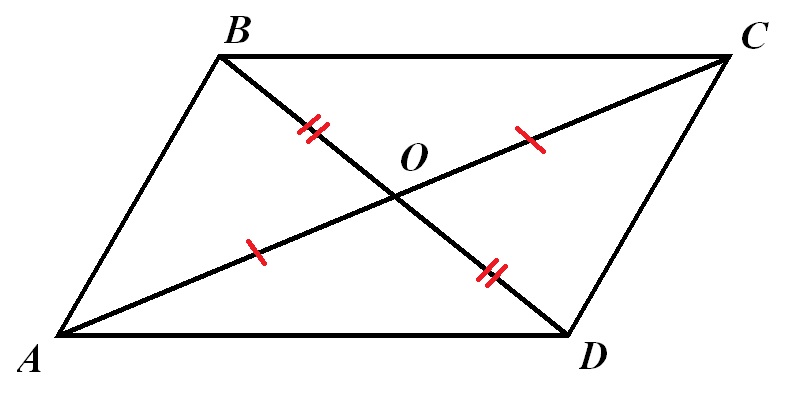
Чертеж во вложении.
Т.к. АО - медиана ∆ВАД, то ВО=ОД.
Т.к. ВО - медиана ∆АВС, то АО=ОС.
таким образом, точка О - середина каждой из диагоналей АС и ВД четырехугольника АВСД. По признаку параллелограмма (если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм) получаем, что АВСД - параллелограмм.