Предмет: Геометрия,
автор: johny3
В треугольник ABC вписан параллелограмм ADEF так, что угол A у них общий, а вершина E лежит на стороне BC. Площадь параллелограмма равна 36 кв.см, а треугольника BDE - 24 кв.см. Найдите площадь треугольника ABC.
Ответы
Автор ответа:
0
пусть высота треугольника DBE равна h2, а параллелограмма h1. заметим, что
высота треугольника FEC тоже равна h1.
имеем AF*h2/2=24 AF*h1=36 разделим первое уравнение на второе и учтем подобие
треугольников ECF и DBE получим что их площади отнрсятся как 16/9
Sfec=9/16*24=13,5
SABC=36+24+13,5=73,5
высота треугольника FEC тоже равна h1.
имеем AF*h2/2=24 AF*h1=36 разделим первое уравнение на второе и учтем подобие
треугольников ECF и DBE получим что их площади отнрсятся как 16/9
Sfec=9/16*24=13,5
SABC=36+24+13,5=73,5
Автор ответа:
0
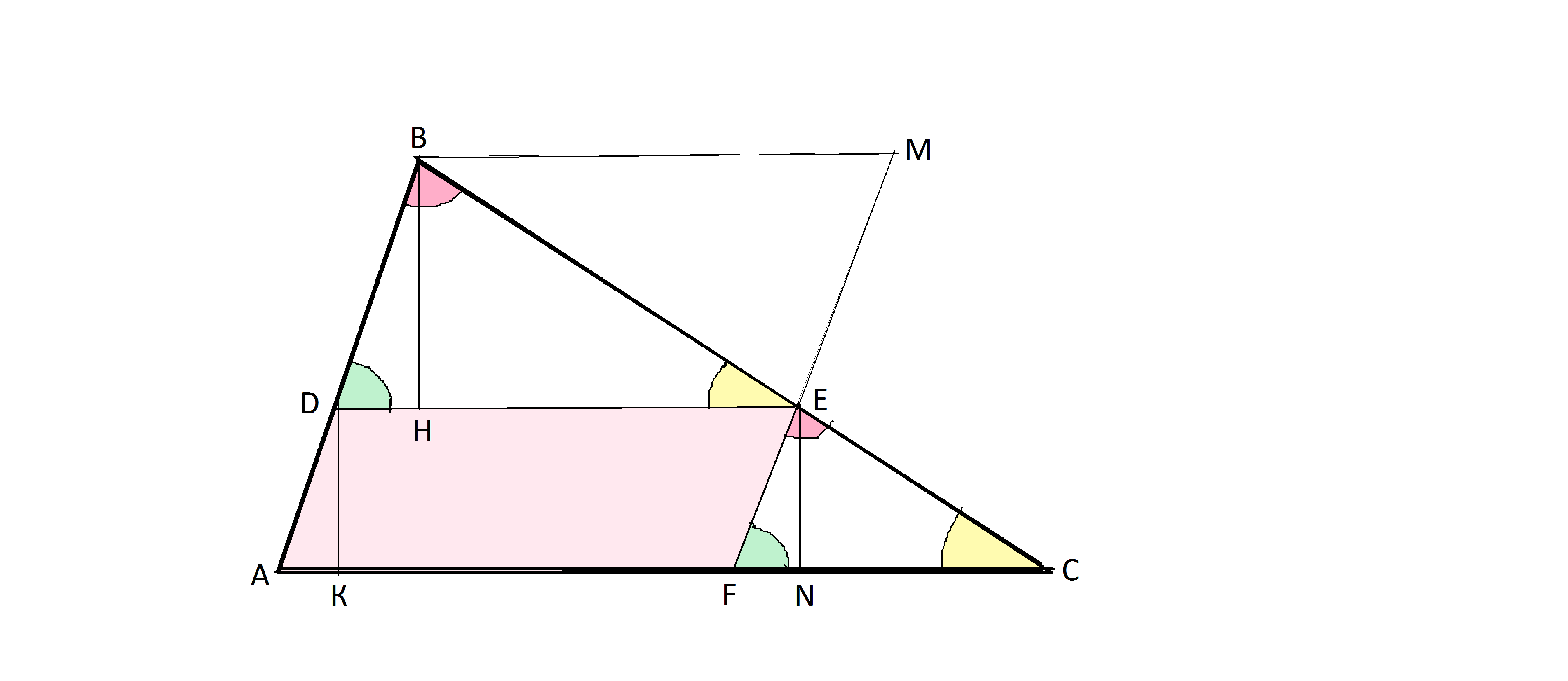
Сделаем рисунок.
Проведем через вершину В прямую параллельно АС,
продолжим FE до пересечения с нею. Точку пересечения обозначим М.
ВМ||D
EDB||ME
DBMЕ - параллелограмм, площадь которого равна 2S ᐃDBE, т.к. диагонель ВЕ делит его пополам. Очевидно, что площади параллелограммов с равной стороной относятся как отношения их высот, проведенных к этой равной стороне.
SDBME:S ADEF= ВН*DE:DK*DE=48:36=4:3
ВН:DK=4:3
Треугольники DBЕ и FEC подобны, т.к. имеют равные углы по свойству параллельных прямых и секущей.
DK=EN, они - перпендикуляры между параллельными прямыми.
Следовательно, высоты подобных треугольников DBЕ и FEC относятся как 4:3.
Площади подобных фигур относятся как квадраты коэффициентов подобия их линейных размеров.
S Δ DBЕ : Δ S FEC =(4/3)² =16/9
Пусть S Δ FEC=х
24:х=16/9
х=13,5
S Δ FEC=13,5 см²
Площадь Δ АВС равна сумме площадей трех фигур: параллелограмма и двух треугольников.
S Δ ABC=36+24+13,5=73,5 см²
Проведем через вершину В прямую параллельно АС,
продолжим FE до пересечения с нею. Точку пересечения обозначим М.
ВМ||D
EDB||ME
DBMЕ - параллелограмм, площадь которого равна 2S ᐃDBE, т.к. диагонель ВЕ делит его пополам. Очевидно, что площади параллелограммов с равной стороной относятся как отношения их высот, проведенных к этой равной стороне.
SDBME:S ADEF= ВН*DE:DK*DE=48:36=4:3
ВН:DK=4:3
Треугольники DBЕ и FEC подобны, т.к. имеют равные углы по свойству параллельных прямых и секущей.
DK=EN, они - перпендикуляры между параллельными прямыми.
Следовательно, высоты подобных треугольников DBЕ и FEC относятся как 4:3.
Площади подобных фигур относятся как квадраты коэффициентов подобия их линейных размеров.
S Δ DBЕ : Δ S FEC =(4/3)² =16/9
Пусть S Δ FEC=х
24:х=16/9
х=13,5
S Δ FEC=13,5 см²
Площадь Δ АВС равна сумме площадей трех фигур: параллелограмма и двух треугольников.
S Δ ABC=36+24+13,5=73,5 см²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: easytop4ick
Предмет: Алгебра,
автор: vikabutlerska
Предмет: Другие предметы,
автор: itachi0216
Предмет: Биология,
автор: snikers2966
Предмет: Физика,
автор: maksivip