Предмет: Геометрия,
автор: 0yanusya0
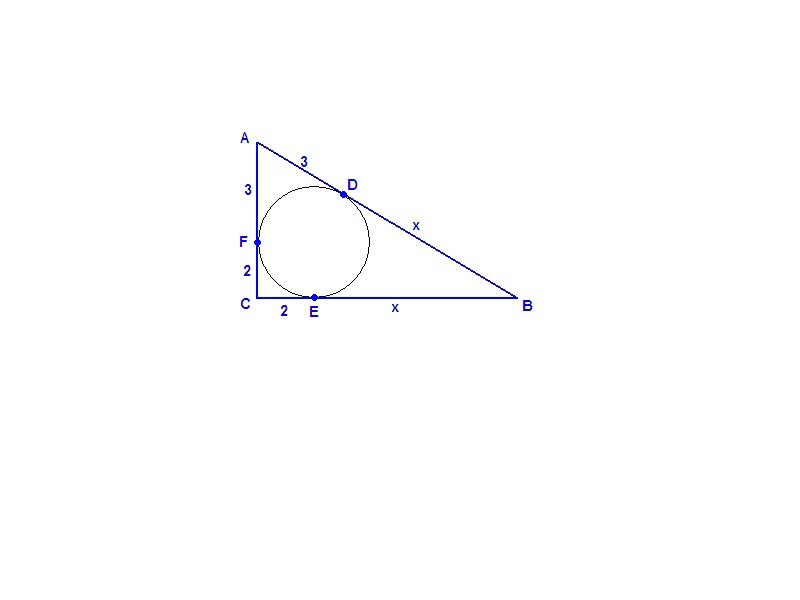
Точка касания окружности, вписанной в прямоугольный треугольник делит катет на отрезки длиной 2см и 3см, считая от прямого угла. Найдите радиус окружности, описанной около треугольника.
Ответы
Автор ответа:
0
Отрезки касательных, проведенных из одной точки, равны:
AD = AF = 3 см
CE = CF = 2 см
BD = BE = x (обозначим)
По теореме Пифагора:
AB² = CA² + CB²
(x + 3)² = 5² + (x + 2)²
x²+ 6x + 9 = 25 + x² + 4x + 4
2x = 20
x = 10
AB = 10 + 3 = 13 см
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы:
R = AB/2 = 6,5 см
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: lina0562
Предмет: География,
автор: 123456712097639
Предмет: Алгебра,
автор: Polous2009
Предмет: Информатика,
автор: Iimpro76
Предмет: История,
автор: JuliaVtul