Question

задание во вложение.

Answer 1

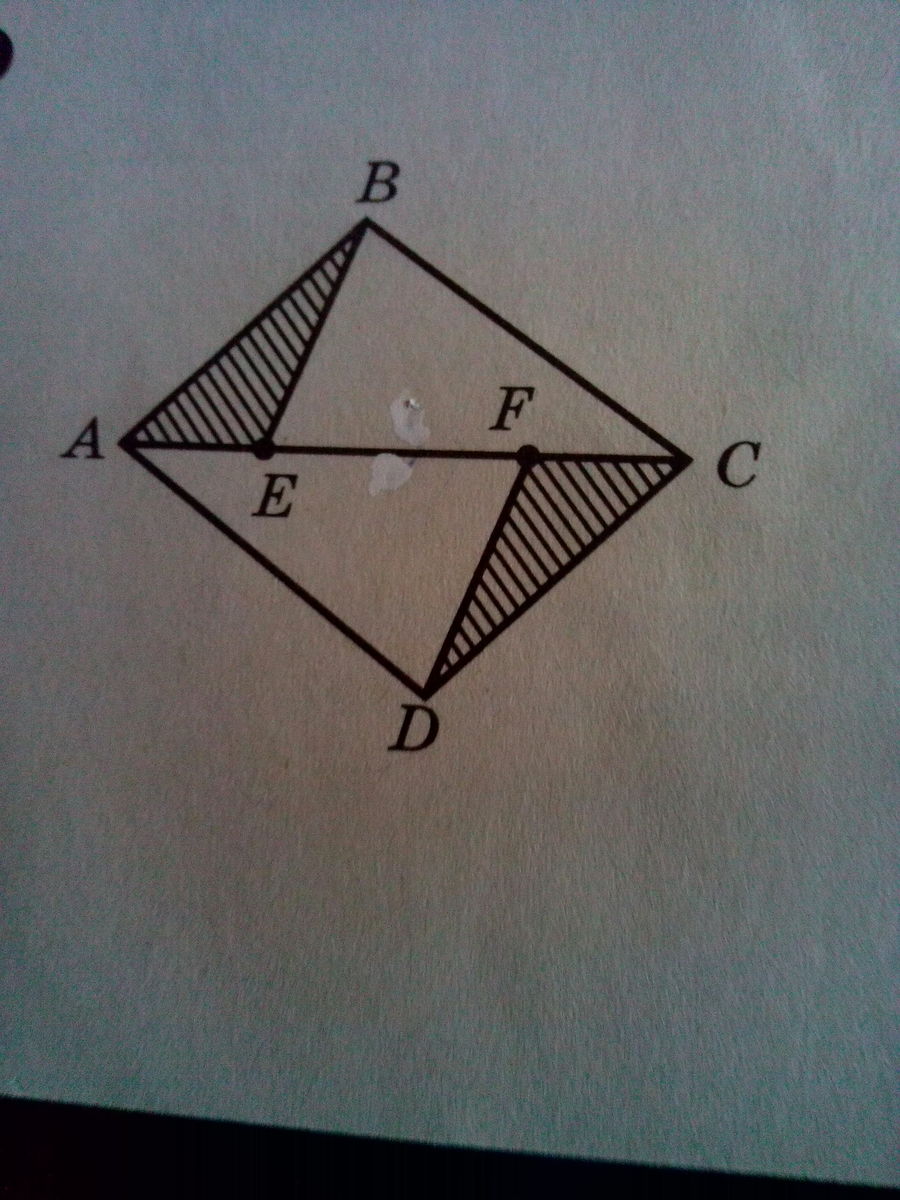
В четырехугольнике АВСD   данном на  рисунке,  
AB||CD 
AB=CD, 
AE=CF.
Докажите, что AD||BC
.--------------------------
Рассмотрим треугольники АВЕ и CDF.
В них равны две стороны и угол между ними: 
АВ=CD
FC=AE
∠BAE=∠FCD
Треугольники, в которых равны две стороны и заключенный между ними угол, равны.
Из равенства этих треугольников следует равенство ВЕ=FD
Рассмотрим треугольники АFD и ВЕС. 
У них  ∠ АFD = ∠BEF как дополняющие равные углы ∠ВЕА и ∠DFC до 180°  Сторона АF одного равна стороне  ЕС другого, как состоящие из равных отрезков ( ЕF - общий отрезок и АЕ=FC) 
Треугольники, в которых равны две стороны и заключенный между ними угол равны.
Треугольнике ВЕС и AFD равны.
Следовательно, ВС=AD
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.  
У параллелограмма противоположные стороны параллельны. 
AD||BC,  что и требовалось доказать.  

Answer 2

СПАСИБО))))))))))))))))))))))))))))))

Answer 3

чтобы доказать, что  AD||BC. докажем что ABCD
1) Рассмотрим треугольники АВЕ и CDF.
АВ=CD ( по условию)
FC=AE ( по условию)
∠BAE=∠FCD ( и они накрест лежащие при AB||CD и секущей АС)
зн. треугольники АВЕ и CDF равны  ( по 1 признаку)
зн.  ВЕ=FD ( т.е. треугольники АВЕ и CDF равны)
2) Рассмотрим треугольники АFD и ВЕС.
 ∠ АFD = ∠BEF
АF= ЕС
ЕF - общий
зн. треугольники АFD и ВЕС равны ( по 1 признаку)
зн. ВС=AD
зн. ABCD параллельны
зн. AD||BC
теорема доказана