Предмет: Геометрия,
автор: ruslanpetrov
в трапеции ABCD (AD и BC-основания) точка K лежит на стороне CD, причем CK:KD=1:2. AK пересекает BD в точке O. Докажите, что если BC:AD=1:2, то BO=OD
Ответы
Автор ответа:
0
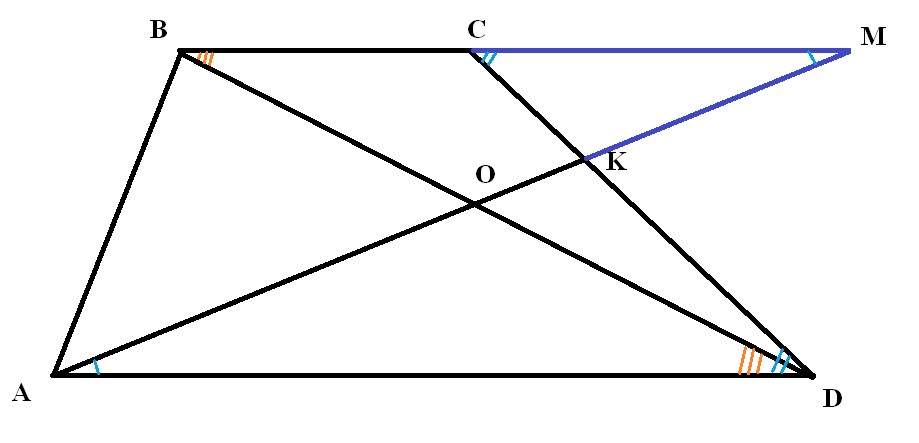
Чертеж во вложении.
пусть М - точка пересечения продолжений прямых АК и ВС.
∆СКМ и ∆ДКА подобны по двум углам. Значит,

Рассмотрим ∆ВОМ и ∆АОД. У них ВМ=АД (по доказанному выше), ∠В=∠Д, ∠M=∠A.
Значит, ∆ВОМ = ∆АОД по стороне и прилежащим углам. Из этого равенства следует, что ВО=ОД.
Доказано.
пусть М - точка пересечения продолжений прямых АК и ВС.
∆СКМ и ∆ДКА подобны по двум углам. Значит,
Рассмотрим ∆ВОМ и ∆АОД. У них ВМ=АД (по доказанному выше), ∠В=∠Д, ∠M=∠A.
Значит, ∆ВОМ = ∆АОД по стороне и прилежащим углам. Из этого равенства следует, что ВО=ОД.
Доказано.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: angelinabelskaa754
Предмет: Английский язык,
автор: Ksenia11064
Предмет: Информатика,
автор: Аноним
Предмет: Химия,
автор: химзад
Предмет: Физика,
автор: PlisDar