Question

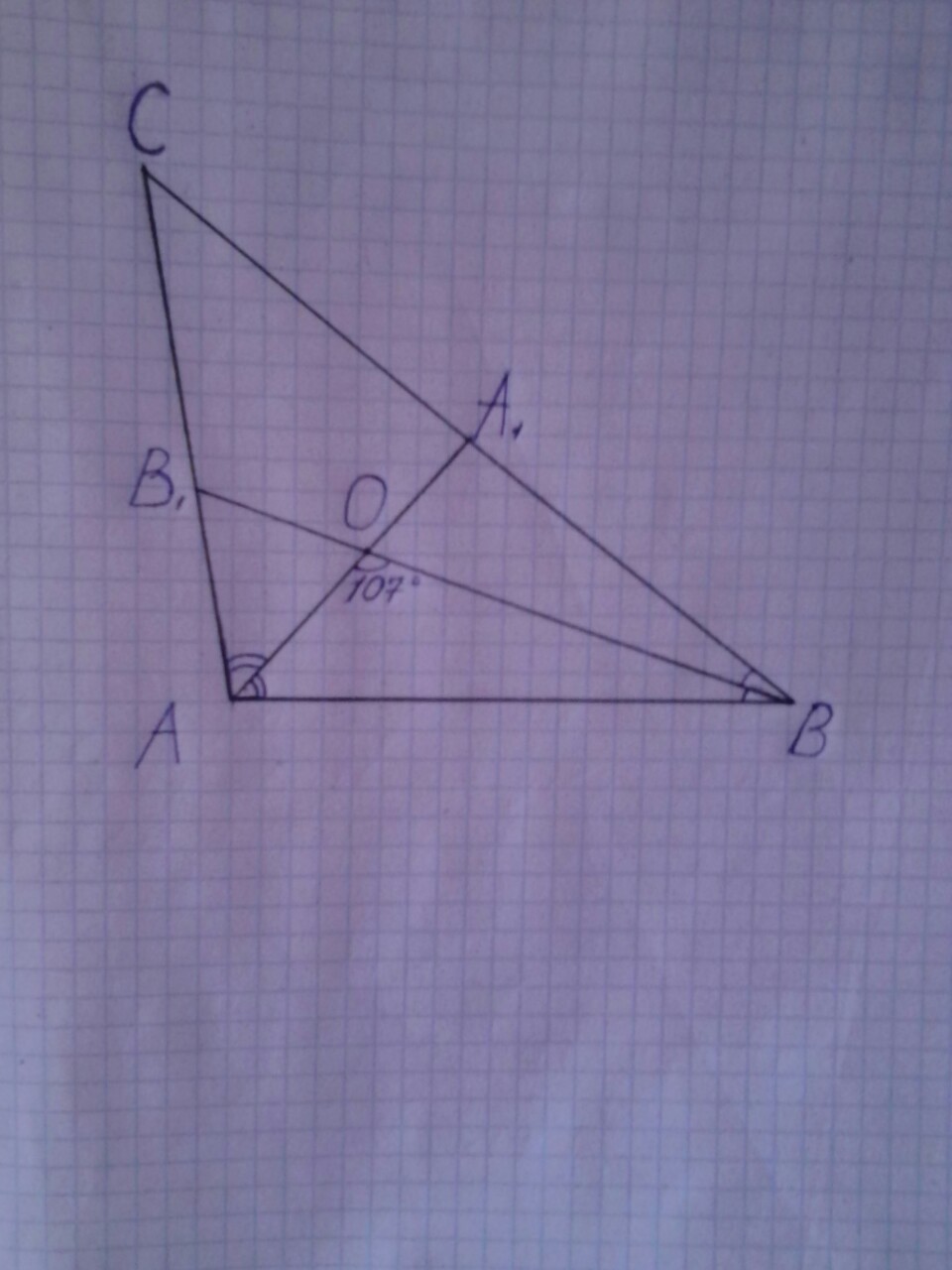
Дано: ΔABC, AA1, BB1 - биссектрисы. AA1∩BB1=0. ∠ABC=30, ∠AOB=107°.
Доказать: ΔABC не является остроугольным.
С ПОДРОБНЫМ ОБЪЯСНЕНИЕМ!

Answer 1

Рассмотрим  Δ АОВ. ∠AOB=107° - по условию. Так как ВВ1 биссектиса и делит угол АВС пополам     ∠ АВО= 1/2∠АВС=1/2*30=15°

Сумма углов  треугольника  равна 180°. ∠ ОАВ=180-107-15=58°

Рассмотрим  Δ АВС . Так как АА 1 биссектрисса  и делит  угол  САВ пополам, ∠ САВ = 2*∠ОАВ=2*58=116°

∠ АСВ = 180-116-30= 34°

Остроугольный треугольник - это треугольник, в котором все три угла острые, т.е. меньше 90°.

В ΔABC  два острых угла  ∠ АВС=30 °, ∠АСВ=34 °, а ∠САВ=116 °. Значит ΔАВС не острый, а тупоугольный.