Предмет: Алгебра,
автор: N00B1
2 - 2 cos^2x - (корень из 3)sinx = 0 Подскажите пожалуйста, как можно преобразовать (корень из 3)sinx , чтобы придти к cosx. Или что то нужно сделать по другому?
Приложения:
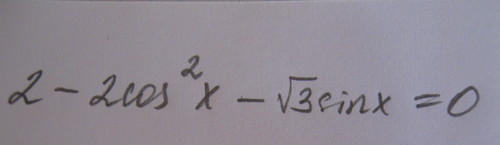
Ответы
Автор ответа:
0
2-2(1-sin²x)-V3sinx=0
2-2+2sin²x-V3sinx=0
2sin²x-V3sinx=0
sinx(2sinx-V3)=0
sinx=0
x=pik
2sinx=V3
sinx=V3/2
x=(-1)^k*arcsinV3/2+pik
x=(-1)^kpi/3+pik
2-2+2sin²x-V3sinx=0
2sin²x-V3sinx=0
sinx(2sinx-V3)=0
sinx=0
x=pik
2sinx=V3
sinx=V3/2
x=(-1)^k*arcsinV3/2+pik
x=(-1)^kpi/3+pik
Автор ответа:
0
Если в уравнении есть одновременно sinx и  либо
либо  и
и  , то нужно выразить из основного тригонометрического тождества " тригонометрическая единица" квадрат синуса или квадрат косинуса.
, то нужно выразить из основного тригонометрического тождества " тригонометрическая единица" квадрат синуса или квадрат косинуса.


Похожие вопросы
Предмет: Химия,
автор: Miа16
Предмет: Русский язык,
автор: liyanevskaya99
Предмет: Физика,
автор: nasyrovakata259
Предмет: Химия,
автор: htcpnone