Предмет: Математика,
автор: Katyunyabondar
Решите логарифмическое неравенство, пожалуйста
Приложения:
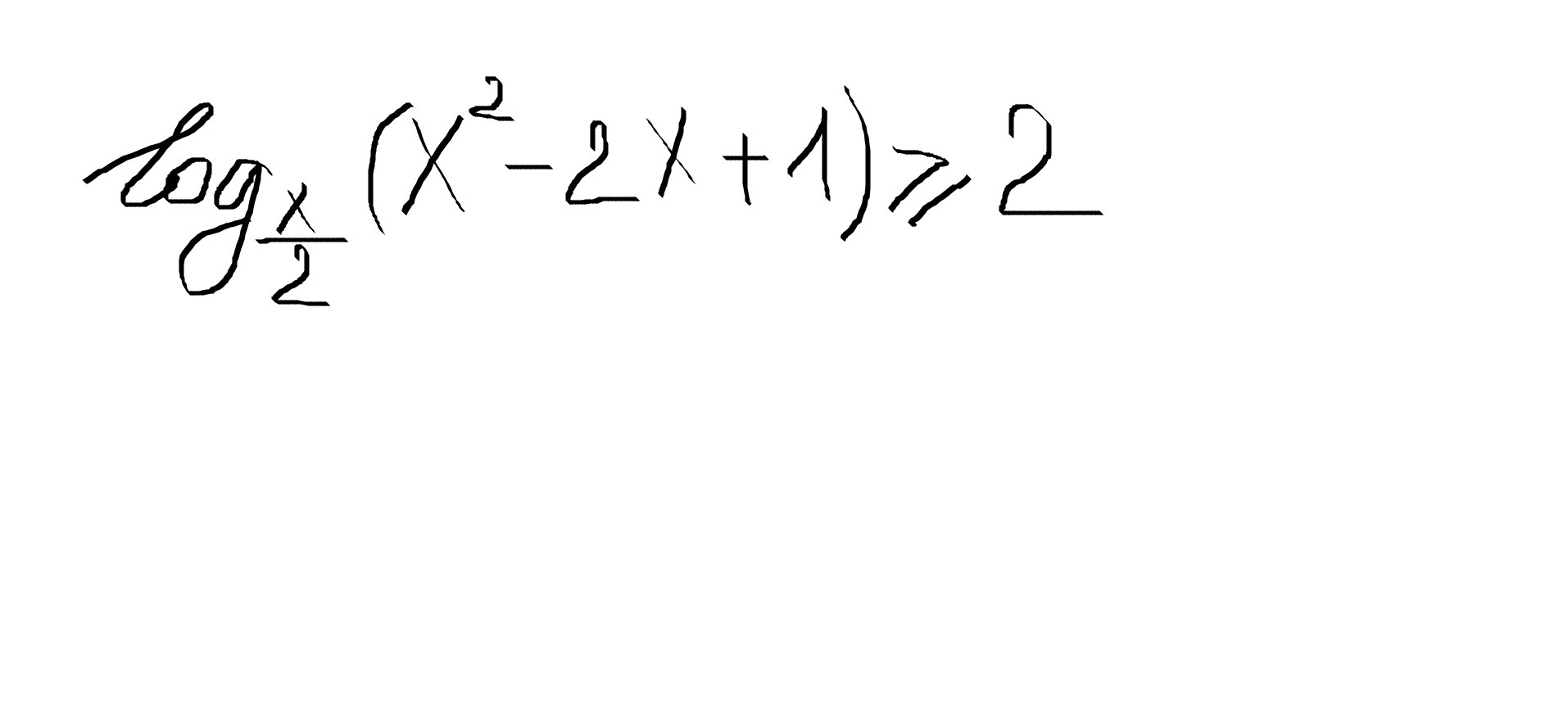
Ответы
Автор ответа:
0
logx/2 (x²-2x+1)≥2
logx/2 (x²-2x+1) ≥ logx/2 (x/2)²
logx/2 (x-1)² ≥ logx/2 (x/2)²
loga(x) f(x) ∨ loga(x) g(x)
(f(x) - g(x))(a(x)-1) ∨ 0
((x-1)² - (x/2)²)(x/2 - 1) ≥ 0
(x-1-x/2)(x-1+x/2)(x/2-1) ≥ 0
(x-2/2)(3x-2/2)(x-2/2) ≥ 0
(x-2/2)²(3x-2/2)0
x∈[2/3;∞)
ОДЗ:
2≠x>0
x²-2x+1>0
x∈ (-∞;∞)
[2/3;1)∪(1;2)∪(2;∞)
logx/2 (x²-2x+1) ≥ logx/2 (x/2)²
logx/2 (x-1)² ≥ logx/2 (x/2)²
loga(x) f(x) ∨ loga(x) g(x)
(f(x) - g(x))(a(x)-1) ∨ 0
((x-1)² - (x/2)²)(x/2 - 1) ≥ 0
(x-1-x/2)(x-1+x/2)(x/2-1) ≥ 0
(x-2/2)(3x-2/2)(x-2/2) ≥ 0
(x-2/2)²(3x-2/2)0
x∈[2/3;∞)
ОДЗ:
2≠x>0
x²-2x+1>0
x∈ (-∞;∞)
[2/3;1)∪(1;2)∪(2;∞)
Похожие вопросы
Предмет: Алгебра,
автор: polinakrepostnova
Предмет: Алгебра,
автор: ronald9690
Предмет: История,
автор: nikita9990top16
Предмет: Литература,
автор: МиленочкаDanilova
Предмет: Литература,
автор: 56723