Предмет: Геометрия,
автор: Аноним
Решите пожалуста!Срочно!!
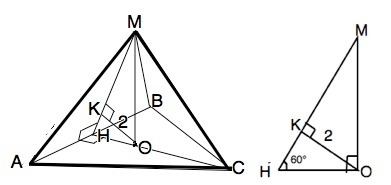
В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 60 градусов. Расстояние от центра основания до боковой грани равно 2 см. Найдите площадь боковой поверхности пирамиды
Ответы
Автор ответа:
0
Пирамида правильная. значит, её основание –правильный треугольник, а боковые грани - равнобедренные треугольники. Если боковые грани правильной пирамиды наклонены под углом 60° к плоскости основания, ⇒ проекции равных наклонных - высот боковых граней, равны радиусу вписанной в основание окружности. НО=r=OK:sin60°
HO=OK:(√3/2)=4/√3
СН - высота АВС. ОС=2•ОН; CH=3•OH=12√3
АС=СН:sin60°=12√3):(√3/2)=24 см - сторона основания.
Апофема МН=ОН:cos60°=8/√3
S бок=h•p/2, где h- апофема, р - полупериметр основания.
S=( 8/√3)•3•24:2=288/√3=96√3 см²
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 08b2007d01
Предмет: Математика,
автор: Lera191929293
Предмет: Физика,
автор: sashakoval7771003
Предмет: Математика,
автор: slavka200440