Предмет: Алгебра,
автор: Умница2003
Докажите тождество, помогите пожалуйста
Приложения:
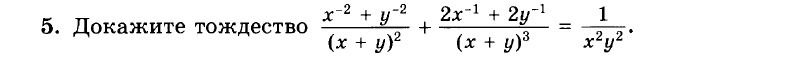
Ответы
Автор ответа:
0
Докажите тождество

Доказательство
Произведем преобразование каждой дроби в левой части уравнения


Находим сумму в левой части

Тождество доказано
Доказательство
Произведем преобразование каждой дроби в левой части уравнения
Находим сумму в левой части
Тождество доказано
Похожие вопросы
Предмет: Математика,
автор: harrypotterhogwarts2
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: N1zel1x
Предмет: Алгебра,
автор: Budgdbd
Предмет: Обществознание,
автор: светлая999