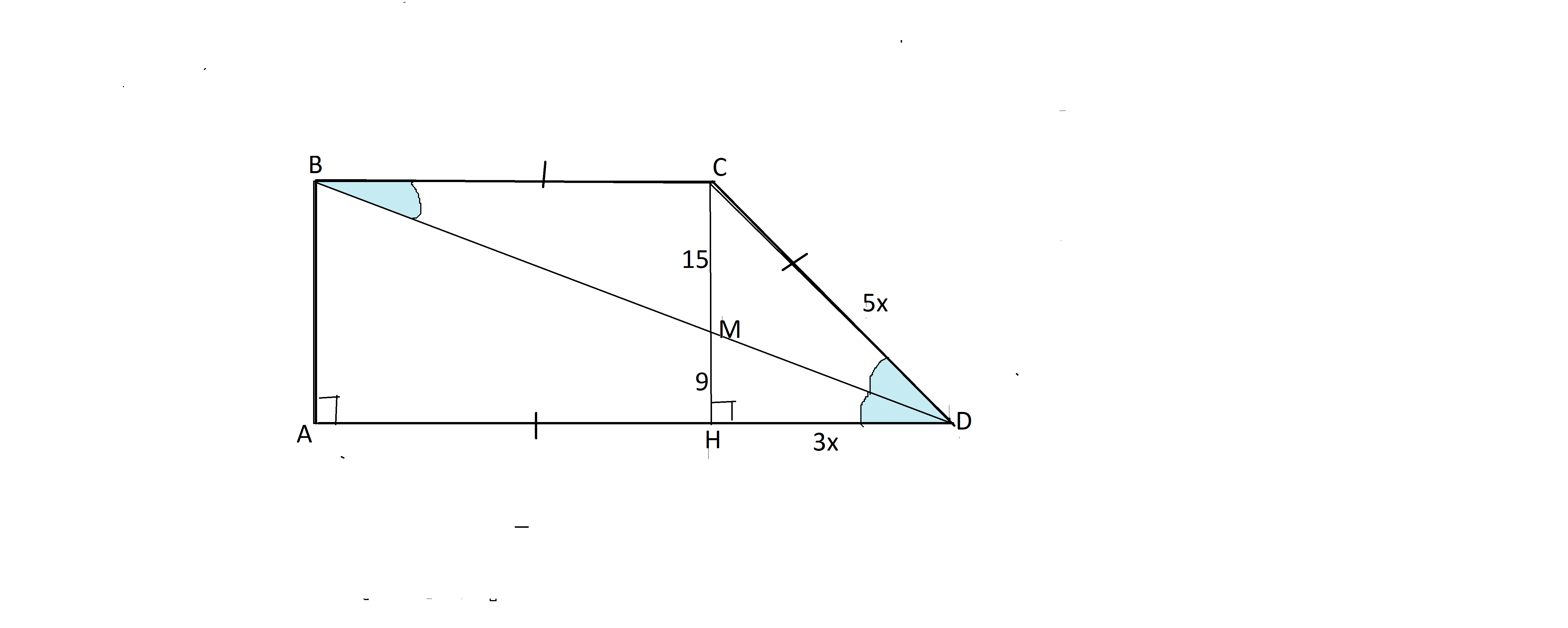
Диагональ прямоугольной трапеции делит острый угол пополам, а высоту, проведенную из вершины тупого угла на отрезки 9 см и 15 см. Найдите периметр трапеции.
Ответы
рассмотрим прямоугольный треугольник АВЕ, где ВЕ высота, значит диагональ отсекает пропорциональные отрезки , пусть AB=15x ,
AE=9x
по теореме пифагора
15+9 = 24
24^2+(9x)^2 = (15x)^2
576+81x^2=225x^2
x=2
Значит сторона АВ=30 . АЕ=18 .
Треуольник АВД подобен АМЕ , где точка М пересечение биссектрисы и высоты, пусть ЕД = у
9/18 = 24/18+y
y=30
значит
значит периметр равен P=2*30+48+24 = 132
В прямоугольной трапеции диагональ=биссектриса острого угла и делит высоту на два отрезка.
Пусть в трапеции АВСD ВС меньшее основание, АD - большее, сторона АВ - перпендикулярна основаниям.
Диагональ ВD - биссектриса угла СDА.
СН - высота из С к АD.
Точка М - пересечение диагонали и высоты трапеции.
Рассмотрим треугольник СНD.
В этом треугольнике биссектриса угла СDН делит противоположную сторону СН на отрезки 15 и 9.
Биссектриса внутреннего угла треугольника делит противоположную сторону
в отношении, равном отношению двух прилежащих сторон.
Следовательно, СD:DН=СМ:МН=15:9 или 5:3, если сократить на 3
Пусть коэффициент отношения сторон ВD и НD будет х.
Тогда СD=5х, DН=3х, и по т.Пифагора
СD²-НD²=СН²
25х²-9х²=576
16х²=576
х²=36
х=6 см
СD=5х=30 см
НD=3х=18 см
В треугольнике ВСD углы СDВ и СВD равны, так как углы ВDА и СВD трапеции равны как накрестлежащие, а ∠СDВ=∠ВDА по условию.
Так как углы при основании ВD треугольника ВСD равны,
треугольник ВСD - равнобедренный и ВС=СD.
АН=ВС как сторона прямоугольника АВСН.
АD=АН+НD=30+18=48 см
Р=АВ+ВС+СD+АD=24+30+30+48=132 см