Предмет: Алгебра,
автор: MilkyWayyy15
Исследовать сходимость ряда
Приложения:
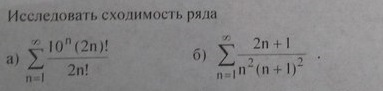
Ответы
Автор ответа:
0
По признаку д'Аламбера:
Данный ряд РАСХОДИТСЯ.
Проверим необходимое условие сходимости ряда:
По первому признаку сравнения данный ряд сходится
Похожие вопросы
Предмет: Математика,
автор: sona788
Предмет: Немецкий язык,
автор: ringo5
Предмет: Химия,
автор: lotos4966
Предмет: Экономика,
автор: Аноним
Предмет: Литература,
автор: лиза8901