Предмет: Алгебра,
автор: Aline2323
найдите наименьшее значение функции g(x)=log0.5(-основание)(2-х^2)
Ответы
Автор ответа:
0
Приложения:
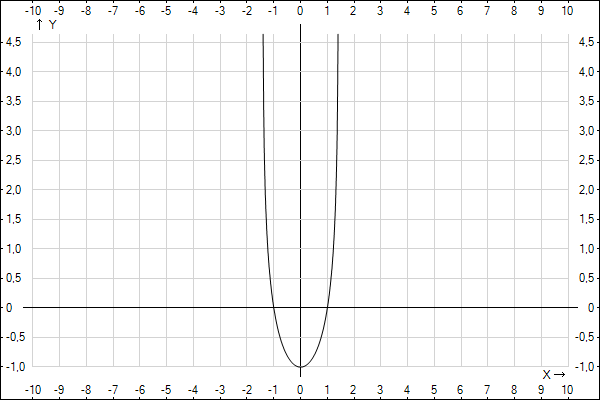
Похожие вопросы
Предмет: Українська мова,
автор: tecnodark278
Предмет: Обществознание,
автор: natfullinaz
Предмет: ОБЖ,
автор: angelinaobieshchyk5
Предмет: Алгебра,
автор: omess
Предмет: География,
автор: Dashulick