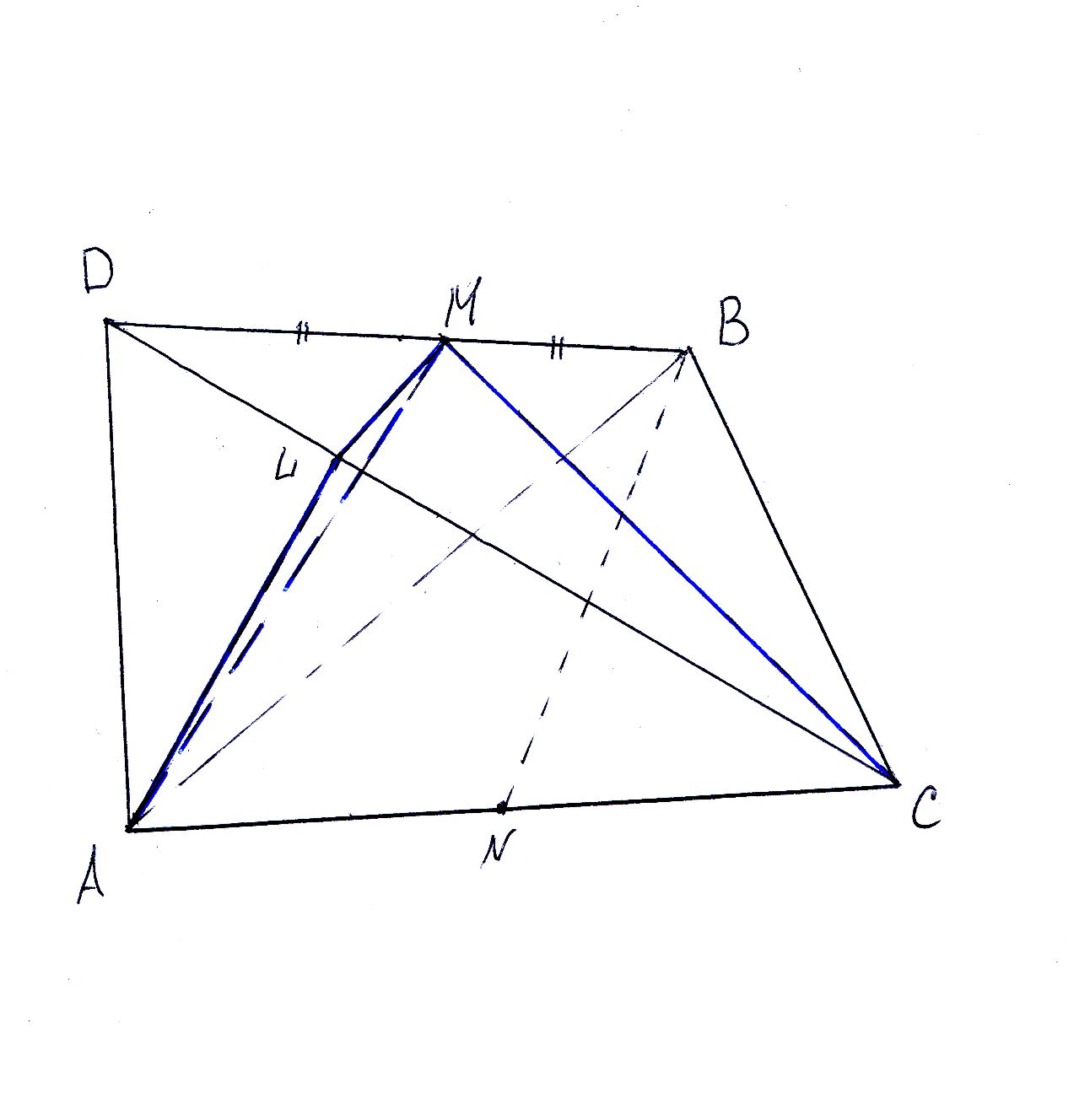
Основанием пирамиды DABC является равнобедренный треугольник ABC с гипотенузой АС=4√2. Ребро АD перпендикулярно плоскости АВС и равно 4. Отрезки АМ и АL являются соответственно высотами треугольников ADB и ADC. Найдите объем пирамиды AMLC.
Желательно с рисунком.
Заранее большое спасибо))
Ответы
Пусть N- середина АС. Тогда BN перпендикулярно плоскости ADC, поскольку BN перпендикулярно АС (медиана равнобедренного треугольника) и AD (BN лежит в плоскости ABC).
BN = AC/2 = 2√2; это - расстояние от точки В до плоскости ADC.
Поскольку точка М лежит на наклонной прямой DB посредине между D и B, расстояние от M до плоскости ADC равно h = BN/2 = √2;
это можно считать высотой пирамиды ALCM , за основание принята грань ALC, осталось сосчитать её площадь.
AL - высота в прямоугольном треугольнике ACD, где AD = 4; AC = 4√2; откуда DC = 4√3;
AL = AD*AC/DC = 4√(2/3);
При этом из подобия ADC и ALC
LC/AL = AC/AD = √2; LC = 8/√3;
Площадь ALC равна S = LC*AL/2 = 16√2/3;
Объем ALCM равен V = S*h/3 = 32/9;
обязательно проверьте всю арифметику