Предмет: Геометрия,
автор: TinyIs
В трапеции ABCD диагонали AC и BD взаимно перпендикулярны, а её средняя линия равна 10 см. Найдите площадь трапеции, если AC=12 см. Пожалуйста распишите решение, если не тяжело!)))
Ответы
Автор ответа:
0
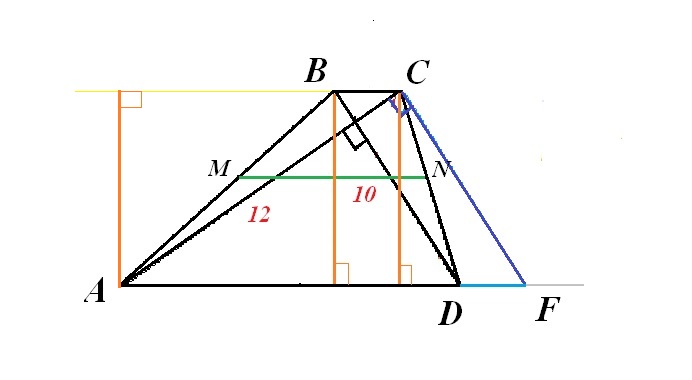
Рисунок к задаче во вложении.
1) Из вершины С трапеции параллельно ВD проведем прямую до пересечения с продолжением АD. Точку пересечения обозначим F.
Так как СF||ВD по построению, а ВС параллельна DF , так как параллельна АD, а DF - продолжение АD, то ВСDF- параллелограмм, значит, ВС= DF.
2) Рассмотрим ∆АВС и ∆СDF. Они имеют равные основания (ВС=DF) и равные высоты (показаны оранжевым цветом), которые равны высоте трапеции. Следовательно, площади ∆АВС и ∆СDF также равны.
3) Площадь трапеции
4) ∆АСF - прямоугольный. По теореме Пифагора
Ответ: 96 см²
Приложения:
Похожие вопросы
Предмет: География,
автор: larisagulega
Предмет: Алгебра,
автор: viktorijacofij
Предмет: Физика,
автор: eva991188
Предмет: Информатика,
автор: КотЕйКАн
Предмет: География,
автор: wwv