Предмет: Математика,
автор: Аноним
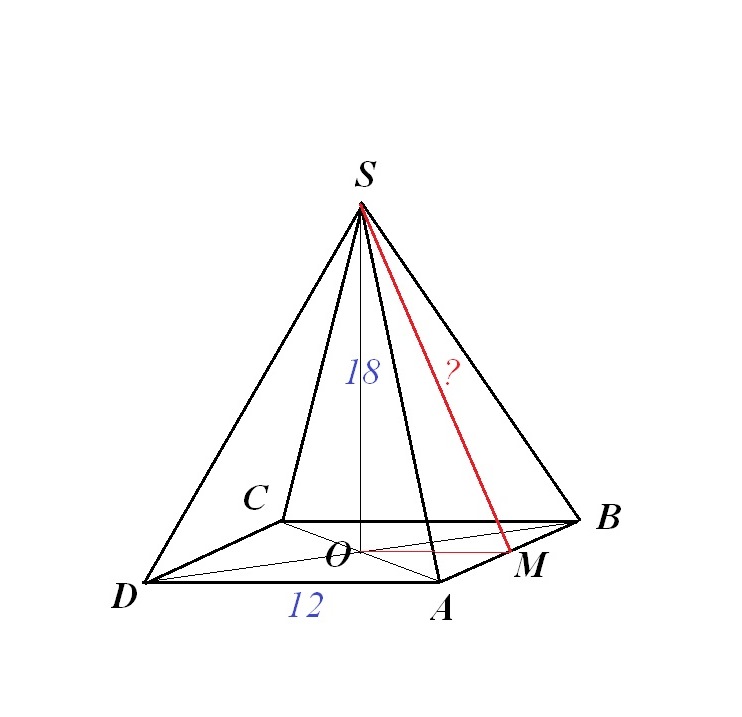
Сторона основания правильной четырёхугольной пирамиды равна 12, а высота пирамиды равна 18. найдите апофему этой пирамиды
Ответы
Автор ответа:
0
В основании пирамиды лежит квадрат. Значит, AB=BC=CD=AD=12.
Т.к. пирамида правильная, то боковые грани - равные друг другу равнобедренные треугольники. Следовательно, апофема пирамиды является медианой, биссектрисой и высотой боковой грани. Значит, АМ=ВМ=6.
В прямоугольном ∆АВС по теореме Пифагора
В прямоугольном ∆АОМ по теореме Пифагора
В прямоугольном ∆SOM по теореме Пифагора
Ответ:
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: CreeperFun
Предмет: История,
автор: oksanakuzmenko09090
Предмет: Английский язык,
автор: Fl0zEnYT
Предмет: История,
автор: Nasyyaaaa