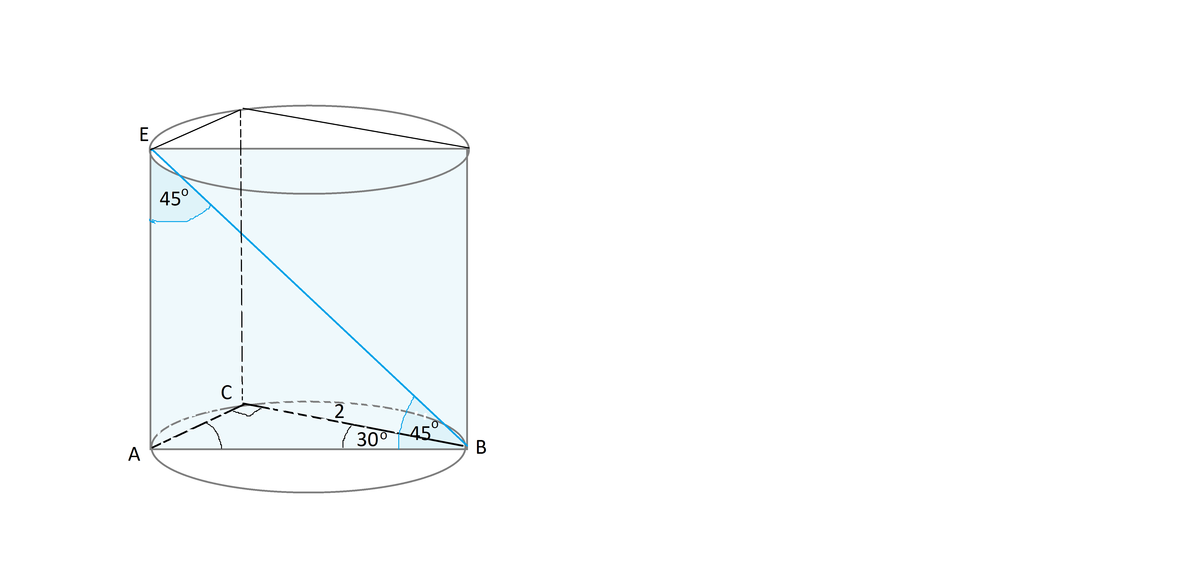
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.
Ответы
Чертеж к задаче во вложении.
∆ АВС - прямоугольный, ∠С=90°, ∠А=30°. Следовательно, гипотенуза АВ является диаметром описанной окружности (основания цилиндра) и АВ=2ВС. По теореме Пифагора
Рассмотрим прямоугольный ∆ ВАА'. У него по условию ∠B=45°, следовательно ∠А'=90°-45°=45°. Поэтому ∆ ВАА' - равнобедренный с основанием BА'. Значит,
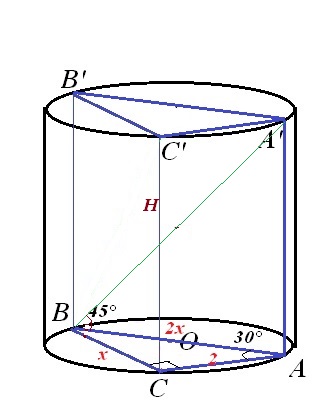
Основанием вписанной в цилиндр призмы служит прямоугольный треугольник. Он вписан в круг - основание цилиндра.
Гипотенуза вписанного прямоугольного треугольника - диаметр окружности, в которую он вписан.
Диаметр АВ =ВС: cos( 30°)
АВ=2:(√3 : 2)=4:√3=4:√3
По условию диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°.
Большая боковая грань призмы имеет основанием большую сторону основания - гипотенузу АВ.
Отсюда высота АЕ цилиндра, как катет ЕА равнобедренного прямоугольного треугольника ЕАВ равна АВ и равна 4:√3
V=πr²H
r=0,5*4:√3 =2:√3
V=π(2:√3 )²(4:√3)=π4*4: 3√3=16π√3:3*3=16π√3):9