Построить равнобедренный треугольник по основанию и высоте, проведённой из вершины при основании.
Ответы
Высота, проведённая из вершины при основании - это высота к боковой стороне треугольника.
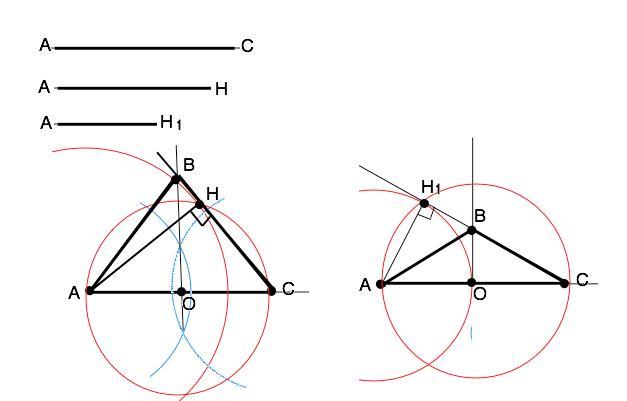
На произвольной прямой циркулем откладываем отрезок АС, равный заданной длине основания треугольника. По общепринятой методике строим срединный перпендикуляр этого отрезка, который пересекает его в т.О. АО=CО. Из т.А чертим окружность, радиус которой равен заданной длине высоты АН. Основание Н высоты будет расположено на построенной окружности. Т.к.высота должна быть перпендикулярна боковой стороне треугольника, на АВ как на диаметре с центром в т.О чертим окружность. Точку ее пересечения с первой окружностью обозначим Н. Угол АНС=90°, т.к. опирается на диаметр.
Проводим прямую из т. С через т. Н до пересечения со срединным перпендикуляром в т. В. Соединяем точки А и В. Искомый треугольник АВС с заданным основанием АС и высотой АН из вершины А при основании построен. В нем основание АВ равно заданной длине, треугольники АОВ=ВОС по двум катетам, следовательно, АВ=СВ, отрезок АН перпендикулярен боковой стороне и равен длине заданной высоты.
В зависимости от длины высоты при равном основании треугольник может получиться как остроугольным, так и тупоугольным, тогда высота из острого угла при основании пересечётся с продолжением боковой стороны.