Question

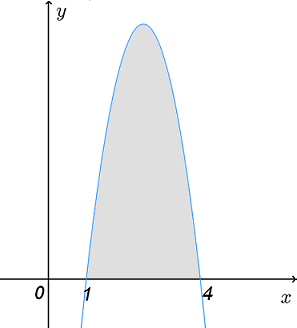
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=−x3+7,5x2−12x+8,5 — одна из первообразных функции f(x).

 

Найдите площадь закрашенной фигуры.

Answer 1

Найдите площадь закрашенной фигуры.

S =  F(x) |[1;4] = −x^3+7,5x^2−12x+8,5 |[1;4] =

   = −4^3+7.5*4^2−12*4+8.5 - (−1^3+7.5*1^2−12*1+8.5) =13.5

ОТВЕТ 13.5

Answer 2

Площадь данной фигуры равна разности первообразных

S = F(4) - F(1) = (−4^3+7,5* 4^2−12*4+8,5) - (−1^3+7,5*1^2−12*1+8,5) = 13.5 ед^2

Ответ: 13.5 ед^2

Я так понимаю это задание из яндекса, сам его ночью видел. Там есть подробное решение тоже