Предмет: Алгебра,
автор: obyava12
Решите неравенство пожалуйста
Приложения:
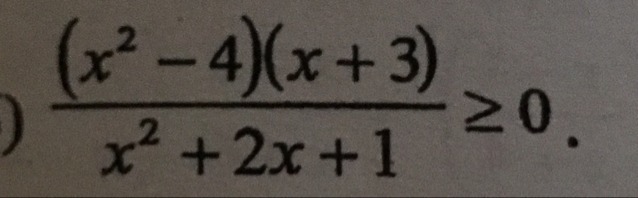
Ответы
Автор ответа:
0
(x^2-4)(x+3) / x^2+2x+1 >=0
Для начала свернём квадрат суммы в знаменателе:
(x^2-4)(x+3) / (x+1)^2 >=0
Затем разделим уравнение на 2 части:
{(x^2-4)(x+3) >=0
{(x+1)^2 >=0
{(x^2-4)(x+3) <=0
{(x+1)^2 <0
Поскольку левая часть всегда неотрицательна, утверждение ложно для всех значений x
{x принадлежит [-3, -2]U[2, +бесконечность)
{x принадлежит R \ {-1}
{x принадлежит (-бесконечности, -3]U[-2, 2]
{x принадлежит пустому множеству (кружок, через центр которого пересекается палка)
Ответ: x принадлежит [-3, -2]U[2, +бесконечности)
Для начала свернём квадрат суммы в знаменателе:
(x^2-4)(x+3) / (x+1)^2 >=0
Затем разделим уравнение на 2 части:
{(x^2-4)(x+3) >=0
{(x+1)^2 >=0
{(x^2-4)(x+3) <=0
{(x+1)^2 <0
Поскольку левая часть всегда неотрицательна, утверждение ложно для всех значений x
{x принадлежит [-3, -2]U[2, +бесконечность)
{x принадлежит R \ {-1}
{x принадлежит (-бесконечности, -3]U[-2, 2]
{x принадлежит пустому множеству (кружок, через центр которого пересекается палка)
Ответ: x принадлежит [-3, -2]U[2, +бесконечности)
Автор ответа:
0
Решение смотри на фото
Приложения:
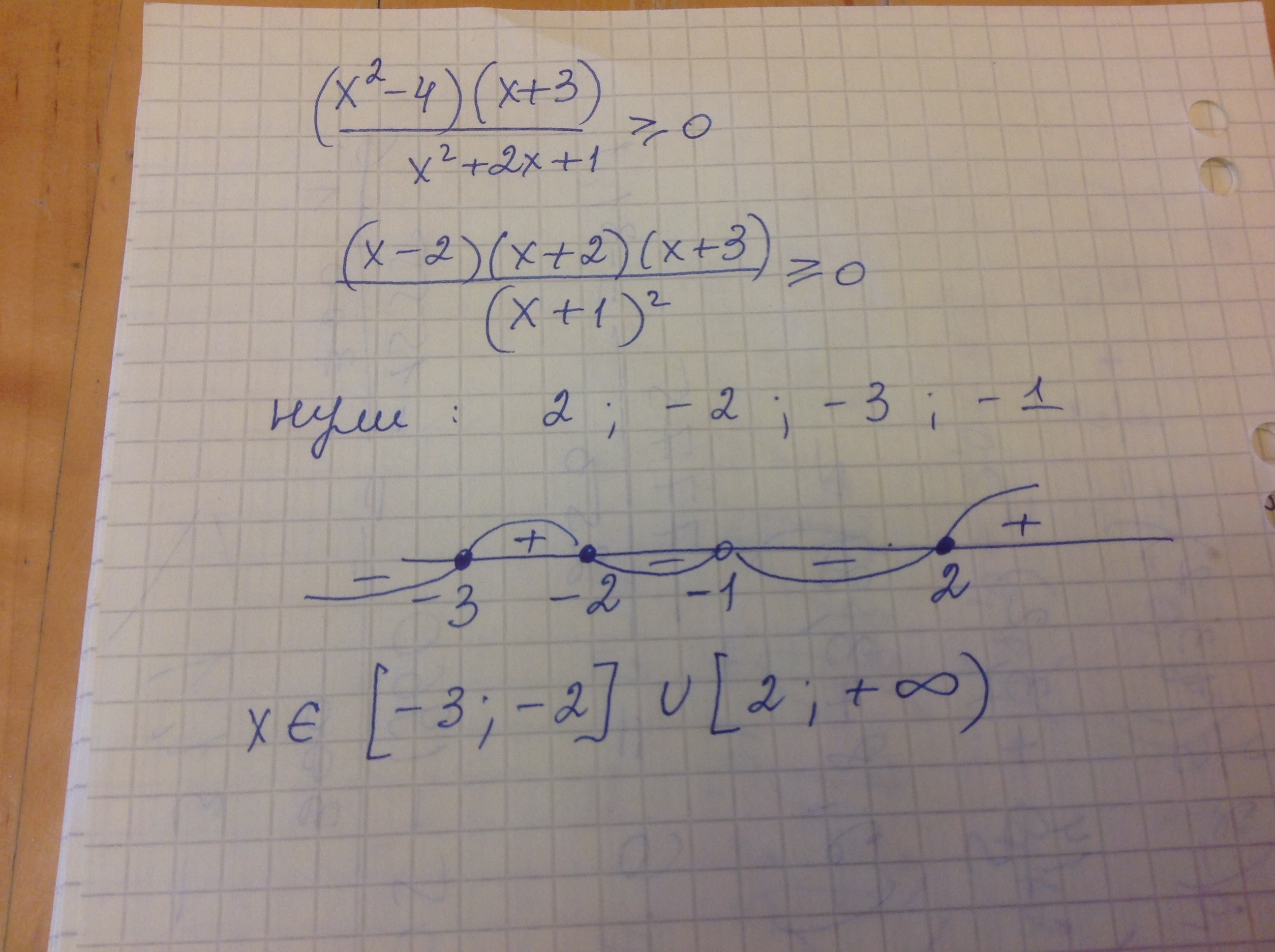
Похожие вопросы
Предмет: Английский язык,
автор: evochka0205
Предмет: Українська мова,
автор: Margorita225
Предмет: География,
автор: Аноним
Предмет: Литература,
автор: ggss77797
Предмет: Математика,
автор: catherinestarowerova