Question

Дано куб ABCDA1B1C1D1 точки M і N на ребрах AA1і CC1 відповідно. Чи проходить площина (MB1N) через вершину D якщо
AM=MA1 CN=NC1?

Answer 1

Примем сторону куба равной а. 

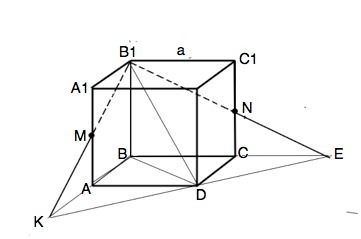
Проведем сечение через В1МN. Оно пересекает плоскость, содержащую грань ABCD,  в точках К - на продолжении АВ, и Е - на продолжении ВС. 

∆ КВЕ - проекция ∆ КВ1Е на плоскость, содержащую основание куба. 

АМ=МА1; CN=NC1 ( дано)

АМ - средняя линия ∆ КВВ1. ⇒ ВК=2а

CN- средняя линия  ∆ ВСВ1 ,⇒ ВЕ=2а. 

∆КВЕ - равнобедренный прямоугольный. Углы при КЕ=45°

КЕ=ВЕ:sin45°=2a√2

По свойству медианы прямоугольного треугольника медиана (высота, биссектриса) ∆ КВЕ=2a√2:2=a√2

Диагональ ВD  квадрата АВСD=а√2  

Медиана ∆ КВЕ совпадает с  ВD. 

Следовательно, плоскость MB1N проходит через вершину D куба. 

      * * * 

Формула диагонали куба а√3. Можно доказать, что медиана ∆ КВ1Е равна а√3 и поэтому совпадает с диагональю куба В1D.