Помогиииите пожалуйста!!
Дан усеченный конус, радиусы основания котрого равны 18 и 30, а образующая 20. Найти расстояние от середины меньшего основания до окружноти большего.
Ответы
Если тебе надо найти высоту, то вот что получается h=корень из 20^2-(30-18)^2
h=16
Теперь от центра малой до большой окружности высота равна 16 а радиус большей равен 30
по теореме Пифагора у нас получается, что 30^2+16^2=34
диагональ равна 34
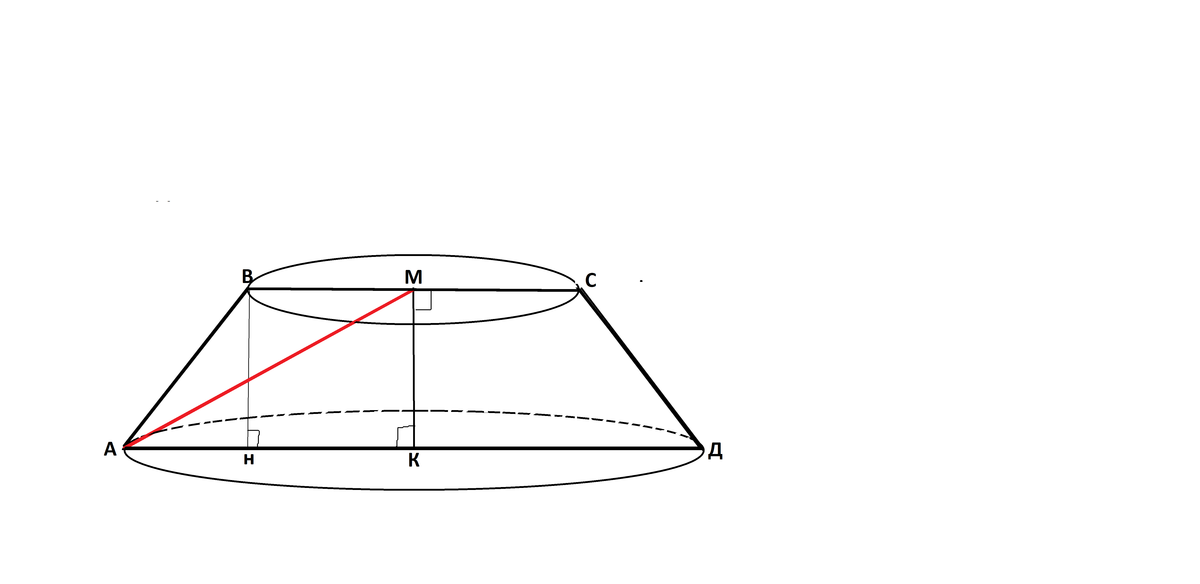
Построим осевое сечение данной в условии фигуры.
Осевое сечение усеченного конуса - это равнобедренная трапеция ( образующие - боковые стороны, основания - диаметры оснований усеченного конуса).
Рисуем равнобедренную трапецию АВСД .
Из центра М верхнего основания опустим перпендикуляр МК к середине нижнего основания.
Получилась прямоугольная трапеция АВМК, равная половие осевого сечения. Углы ВМК и МКА - прямые.
Из М проведм к А прямую.
Эта прямая АМ и есть искомое расстояние от середины меньшего основания до окружноти большего.
А для трапеции АВМК это диагональ АМ.
И найти ее нужно из прямоугольного треугольника АМК, где АМ - гипотенуза, АК и МК - катеты.
Из вершины В опустим высоту ВН к большему основанию.
Из прямоугольного треугольника АВН, где АН - разность радиусов оснований,
т.е.АН=30-18=12, найдем высоту ВН по т. Пифагора ( или обратив внимание, что треугольник АВН - египетский с отношением сторон 3:4:5).
ВН=16
Так как МК = ВН,
АМ²=АК²+МК²=900+256=1156
АМ=√1156=34
Ответ: расстояние от середины меньшего основания до окружноти большего равно 34