Предмет: Геометрия,
автор: aleksvina
в усечённый конус вписан шар . Площади верхнего и нижнего оснований конуса 36пи и 64пи. Чему равна площадь поверхности шара?
Ответы
Автор ответа:
0
найдем длины диаметро они же стороны основания трапеций
pir^2=36pi
r=6
piR^2=64pi
R=8
d=2*6=12
D=2*8=16
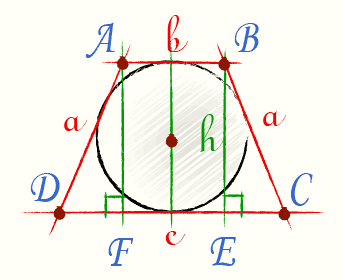
Трапеция являеться ранобедренная так как являеться осевым сечением данного конуса .
поэтому в трапецию можно вписать в окружность то сумма боковых сторон равна сумме оснований
то есть стороны равны по 14 , теперь найдем высоту, а радиус
данного шара будет половина высоты
h=√14^2-2^2=√192
теперь r= √192/2
S=4piR^2 = 192/4*4 pi = 192pi
(2 взялась потому что трапеция равнобедренная то есть 12+2+2=16 ) то есть в сумме они дают нижнее основание!
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: andrejcuktatana1891
Предмет: Алгебра,
автор: romafedko96
Предмет: Алгебра,
автор: almaskotostrofa
Предмет: История,
автор: KabanOFF