Question

На окружности с центром О¹ радиуса r¹ Андрей взял точки М и К. В центральный угол МО¹К он вписал окружность с центром О² радиуса r² . Андрей просит вас, найдите площадь четырёхугольника МО¹КО²!

 

Answer 1

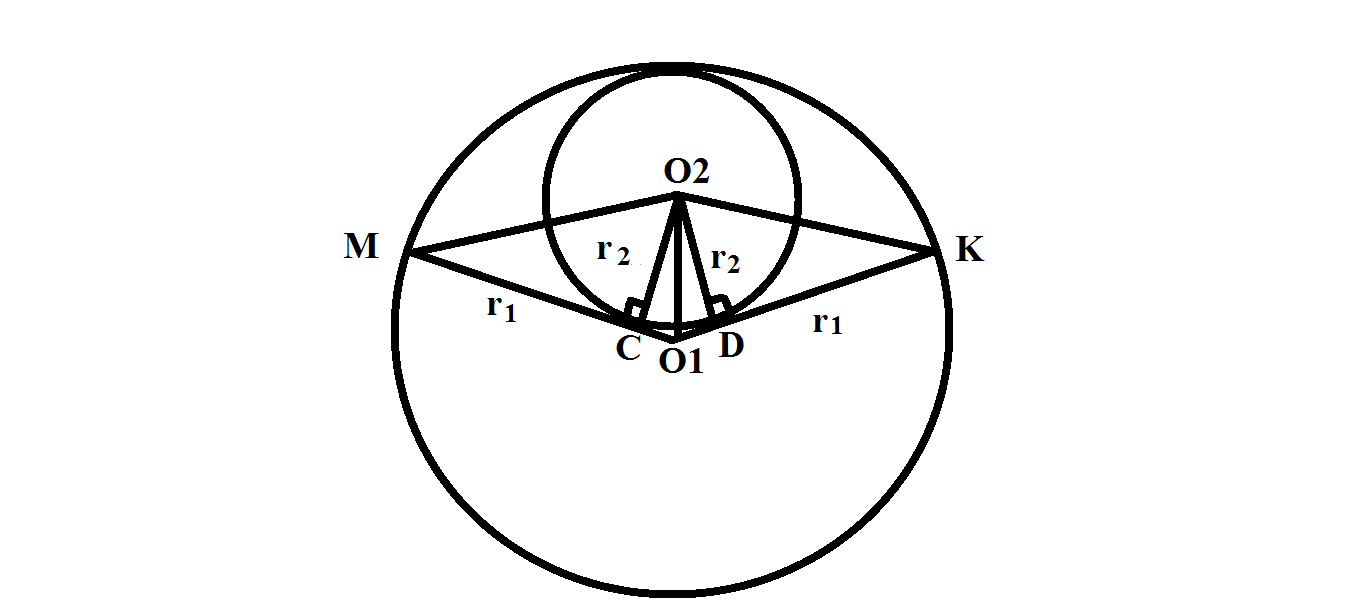
Отрезки касательных к окружности МО₁ и О₁К, проведенные из точки О₁, перпендикулярны к радиусам R₂, проведенным в точки касания С и D.

О₂D = О₂С= R₂ - высоты треугольников Δ МО₁О₂ и Δ О₂О₁К

Отрезки касательных О₁М и О₁К , проведенные из точки О₁, равны и составляют равные углы с прямой О₂О₁, проходящей через точку О₁ и центр окружности О₂

< MO₁O₂=<O₂O₁K

МО₁=О₁К = R₁

О₂О₁ - общая сторона

Δ МО₁О₂ = Δ О₂О₁К ( первый признак равенства треугольников)

S МО₁КО₂= S Δ МО₁О₂ * 2

S Δ = ½ ah

S Δ МО₁О₂ = (½ R₁*R₂)

S МО₁КО₂= (½ R₁*R₂) * 2

S МО₁КО₂=  R₁*R₂