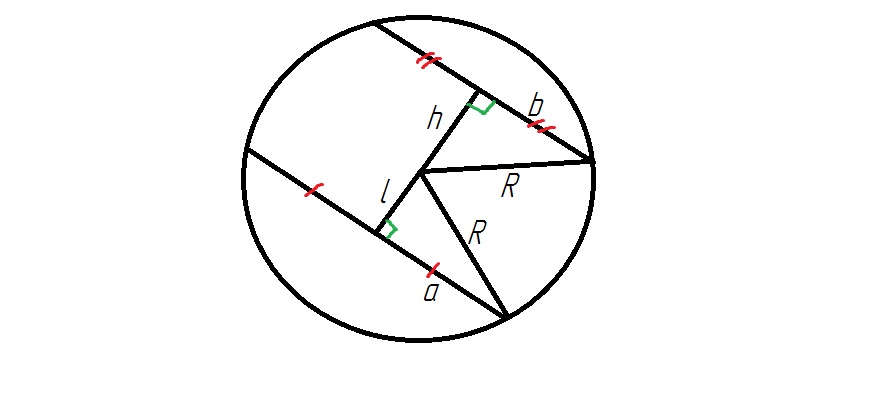
в круге радиусом, равным 10 см ,проведены две параллельные хорды по разные стороны от центра длиною 12 см и 16 см . найдите расстояние между ними
Ответы
Обозначим середины хорд AВ и СD точками К1 и К2
Отрезок соединяющий К1 и К2 проходит через центр окружности О.
Расстояние IК1К2I = IK1OI +IK2OI
Получили два прямоугольных треугольника К1ОВ и К2ОВ
Длина сторон К1В = АВ/2 = 12/2 = 6 см К2D = CD/2 = 16/2 =8
По теореме Пифагора
К1О = корень(ОВ^2-K1B^2) = корень(10^2-6^2) = 8см
К2О = корень(ОD^2-K2D^2) = корень(10^2-8^2) = 6см
IК1К2I = 8+6 = 14 см
Отрезок проведенный к хорде и перпендикулярный ей, делит ее пополам, тогда получаем два прямоугольных треугольника(на рисунке в приложении проведены лишь части отрезков)
Получаем:
где а-половина хорды длинной 16см
где b-половина хорды длинной 12см
Тогда искомое расстояние будет равно:
Ответ: 14см