Предмет: Геометрия,
автор: zagudronov13
Решите пожалуйста!
Две окружности разных радиусов касаются друг друга внешним образом. Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса - в точках C и D. При этом точки A и C лежат на одной касательной, а B и D на другой касательной. Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1,5 и 6.
Ответы
Автор ответа:
0
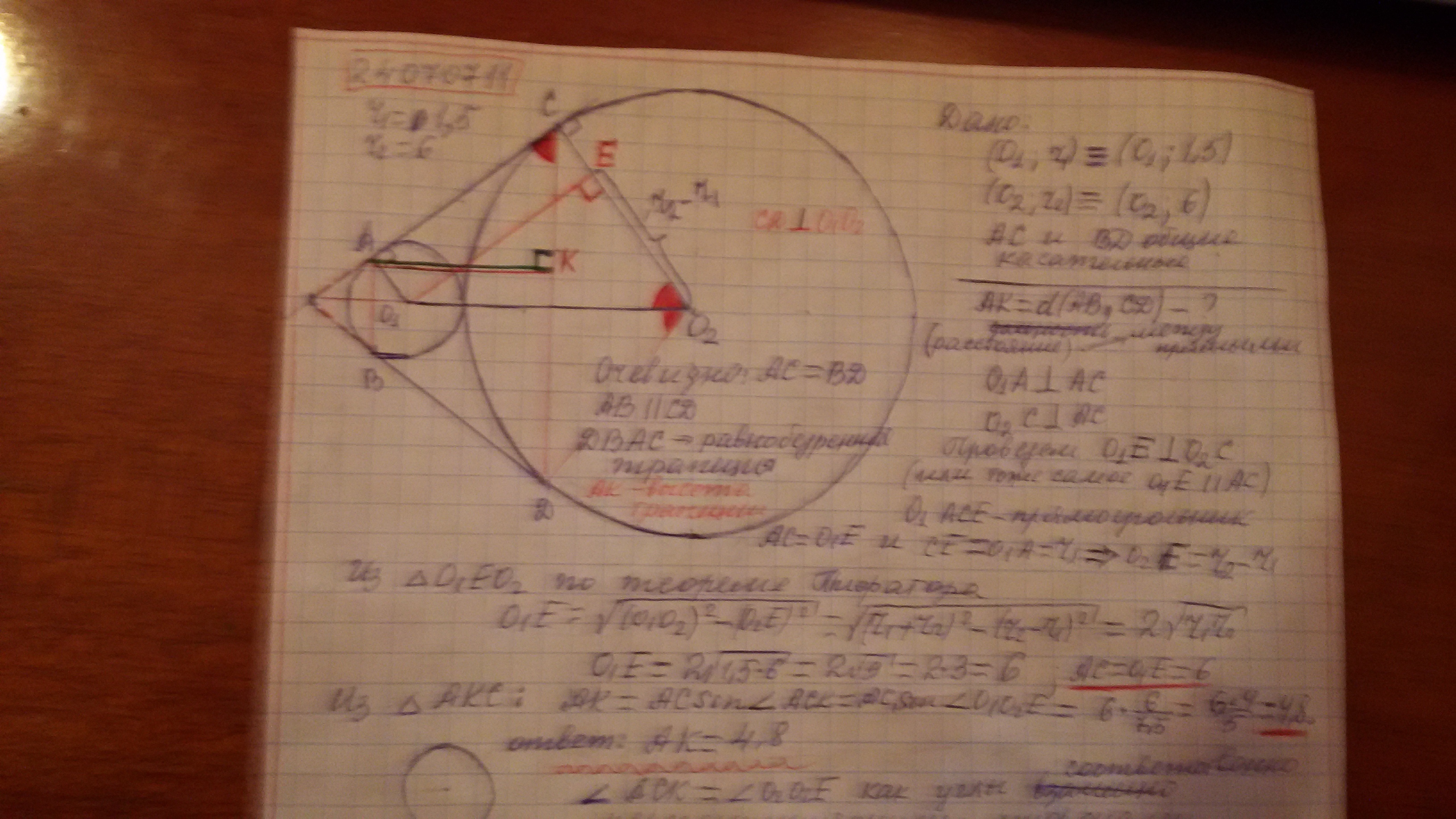
см фото
r₁ =1,5 r₂ =6
∠ACK = ∠O₁O₂E
как углы соответственно перпендикулярными сторонами
CD ⊥ O₁O₂ и CA ⊥ O₂C
O₁O₂ = r₁ + r₂ = 1,5+ 6 =7,5.
DBAC равнобедренная трапеция (BD = AC ; AB || (CD), AK - ее высота .
(расстояние между прямыми AB и CD) .
r₁ =1,5 r₂ =6
∠ACK = ∠O₁O₂E
как углы соответственно перпендикулярными сторонами
CD ⊥ O₁O₂ и CA ⊥ O₂C
O₁O₂ = r₁ + r₂ = 1,5+ 6 =7,5.
DBAC равнобедренная трапеция (BD = AC ; AB || (CD), AK - ее высота .
(расстояние между прямыми AB и CD) .
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sagyndykovali
Предмет: Русский язык,
автор: Matveychikmon
Предмет: Математика,
автор: viola200994
Предмет: Математика,
автор: Suhorukov098
Предмет: Математика,
автор: Школа13