Question

№1
Центральный угол на 25 градусов больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Ответ: 25 градусов
( МНЕ НУЖЕН ХОД РЕШЕНИЯ ЗАДАЧИ)
№2
Найдите вписанный угол, опирающийся на дугу, длина которой равна 1/36 длины окружности. Ответ дайте в градусах
Ответ: 5 градусов
( МНЕ НУЖЕН ХОД РЕШЕНИЯ ЗАДАЧИ)
№3
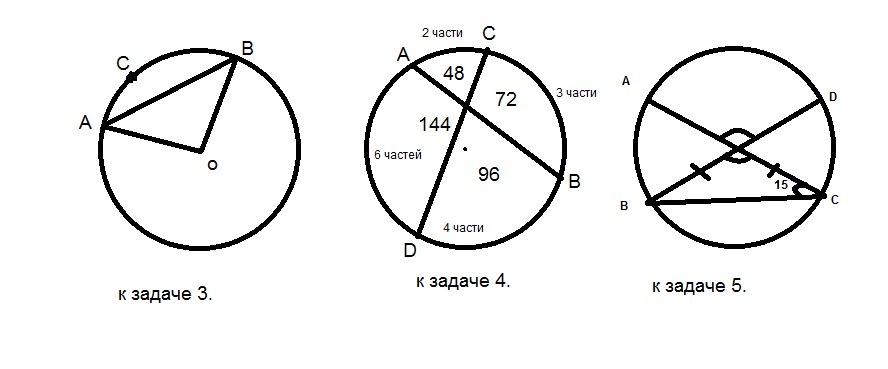
Хорда АВ делит окружность на две дуги, градусные меры которых относятся как 4:5. Под каким углом видна эта хорда из точки С, принадлежащей меньшей дуге окружности? Ответ дайте в градусах. Ответ: 100 градусов.
( МНЕ НУЖЕН ХОД РЕШЕНИЯ ЗАДАЧИ)
№4
Концы пересекающихся хорд АВ И СD делят окружность в отношении АС : СВ : ВD : DА = 2 : 3 : 4 : 6. Найдите величину угла между прямыми АВ и СD. Ответ дайте в градусах. Ответ: 72 градусов.
№5
Отрезки АС и ВD - диаметры окружности с центром О. Угол АСВ равен 15 градусов. Найдите угол АОD. Ответ дайте в градусах.
Ответ: 150 градусов.
( МНЕ НУЖЕН ХОД РЕШЕНИЯ ЗАДАЧИ)

Answer 1

1)обозначим вписанный угол через α, тогда центральный угол равен α+25. вписанный угол составляет половину центрального угла, поэтому  
α=(α+25)/2;
α+25=2α;
2α-α=25;
α=25.
2)Длина окружности вычисляется по формуле C=2πR. По условию,вписанный угол, опирается на дугу, длина которой равна 1/36 длины окружности. L=C*1/36;
L=2πR/36=πR/18;
Длина дугиL вычисляется по формуле L=(2πRn)/180. Подставляем вместо L ранее найденное выражение:
πR/18=πRn/180;
1/18=n/180;
n=10. это величина центрального угла, тогда впписанный угол равен 10/2=5°

3)Из точки C хорда АВ видна под углом АCВ. Пусть большая часть окружности равна 5к, тогда меньшая равна 4к. 5к+4к=360;
9к=360°;
к=360/9=40; Значит меньшая дуга окружности равна 4*40=160°, а большая 5*40=200°
Вписанный угол равен половине дуги, на которую он опирается, значит, опирающийся на большую дугу угол АCВ равен 200°/2=100°.
4)пусть к - коэффициент пропорциональности, тогда 2к+3к+4к+6к=360;
15к=360%
к=360/15=24. градусные меры дуг:
24*2=48°;  24*3=72°;  24*4=96°; 24*6=144.
 угол, составленный двумя хордами равен полусумме дуг, заключенных между его сторонами.  ∠АОС=(48+96)/2=72°.
5) треугольник ВОС равнобедренный (сторонами являются радиусы окружности). углы при основании равнобедренного треугольника равны,∠ОВС=∠ВСО=15°. значит угол ВОС=180-(15+15)=150°. Углы ВОС и АОD вертикальные, поэтому они равны. Величина угла АОD=∠BOC=150°.

 

Answer 2

Проблемка 1 есть, во 2-ой задаче формула, которую мы не проходили. У нас программа 8 -ого класса.