Предмет: Геометрия,
автор: Khristina256
Висота конуса 12 см, радіус його основи 4 см. Площина перпендикулярна до осі конуса перетинає його бічну поверхню конуса по колу довжина якого 6П.Знайдіть відстань від вершини конуса до площини перерізу
Ответы
Автор ответа:
0
Конус (прямой) образуется от вращения прямоугольного треугольника вокруг одного из катетов. Данный конус образован от вращения прямоугольного треугольника АОВ вокруг катета АО. АО является высотой (H= 12см) конуса, ОВ - второй катет - равен радиусу (R= 4 см) основания конуса. АВ - гипотенуза - образующая конуса.
Плоскость, пересекающая боковую поверхность конуса по кругу, отсекает от первоначального конуса меньший конус с вершиной А. Меньший конус образован от вращения меньшего прямоугольного треугольника AO₁B₁, где AO₁ - катет и высота меньшего конуса (искомое расстояние от вершины до плоскости пересечения), О₁В₁ - второй катет - равен радиусу (r) окружности пересечения бОльшего конуса плоскостью. Длина этой окружности L=6π. АB₁ - образующая меньшего конуса.
Угол ОАВ совпадает с углом О₁АВ₁. Угол АОВ и угол АО₁В₁ - прямые ⇒ Угол ABO = Углу АВ₁О₁ ⇒ равны тангенсы углов ABO и АВ₁О₁
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.
AO 12
Tg угла ABO= --------- = --------- = 3
OB 4
AO₁
Tg угла АB₁O₁ = ------------ = 3
O₁B₁
AO₁ = 3 * O₁B₁
Длина окружности = 2 * π * r = 6π ⇒ r = 3 (cм) ⇒ O₁B₁ = 3 (см)
AO₁ = 3 * 3 = 9 (см)
Расстояние от вершины конуса до сечения равно 9 см
Плоскость, пересекающая боковую поверхность конуса по кругу, отсекает от первоначального конуса меньший конус с вершиной А. Меньший конус образован от вращения меньшего прямоугольного треугольника AO₁B₁, где AO₁ - катет и высота меньшего конуса (искомое расстояние от вершины до плоскости пересечения), О₁В₁ - второй катет - равен радиусу (r) окружности пересечения бОльшего конуса плоскостью. Длина этой окружности L=6π. АB₁ - образующая меньшего конуса.
Угол ОАВ совпадает с углом О₁АВ₁. Угол АОВ и угол АО₁В₁ - прямые ⇒ Угол ABO = Углу АВ₁О₁ ⇒ равны тангенсы углов ABO и АВ₁О₁
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.
AO 12
Tg угла ABO= --------- = --------- = 3
OB 4
AO₁
Tg угла АB₁O₁ = ------------ = 3
O₁B₁
AO₁ = 3 * O₁B₁
Длина окружности = 2 * π * r = 6π ⇒ r = 3 (cм) ⇒ O₁B₁ = 3 (см)
AO₁ = 3 * 3 = 9 (см)
Расстояние от вершины конуса до сечения равно 9 см
Автор ответа:
0
Плоскость сечения перпендикулярна оси конуса, основание конуса перпендикулярно оси конуса - эти плоскости параллельны, их радиусы, проведенные в плоскости осевого сечения - параллельны.
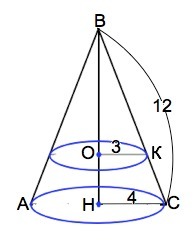
Осевое сечение конуса - равнобедренный треугольник АВС.
. ВН - его высота, Радиус НС=4, ОК - радиус сечения. ВО - расстояние от вершины конуса до плоскости сечения.
Радиус сечения r=6π:2π=3 см
Треугольники ОВК и НВС подобны - прямоугольные с общим острым углом при В.
Из подобия следует отношение ВН:ВО=СН:КО, 12:ВО=4:3, откуда ВО=36:4=9 см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: viktoriyaromanova202
Предмет: История,
автор: werakogan1968
Предмет: Химия,
автор: Marta200666
Предмет: Химия,
автор: Himiaa
Предмет: Информатика,
автор: aren87