Question

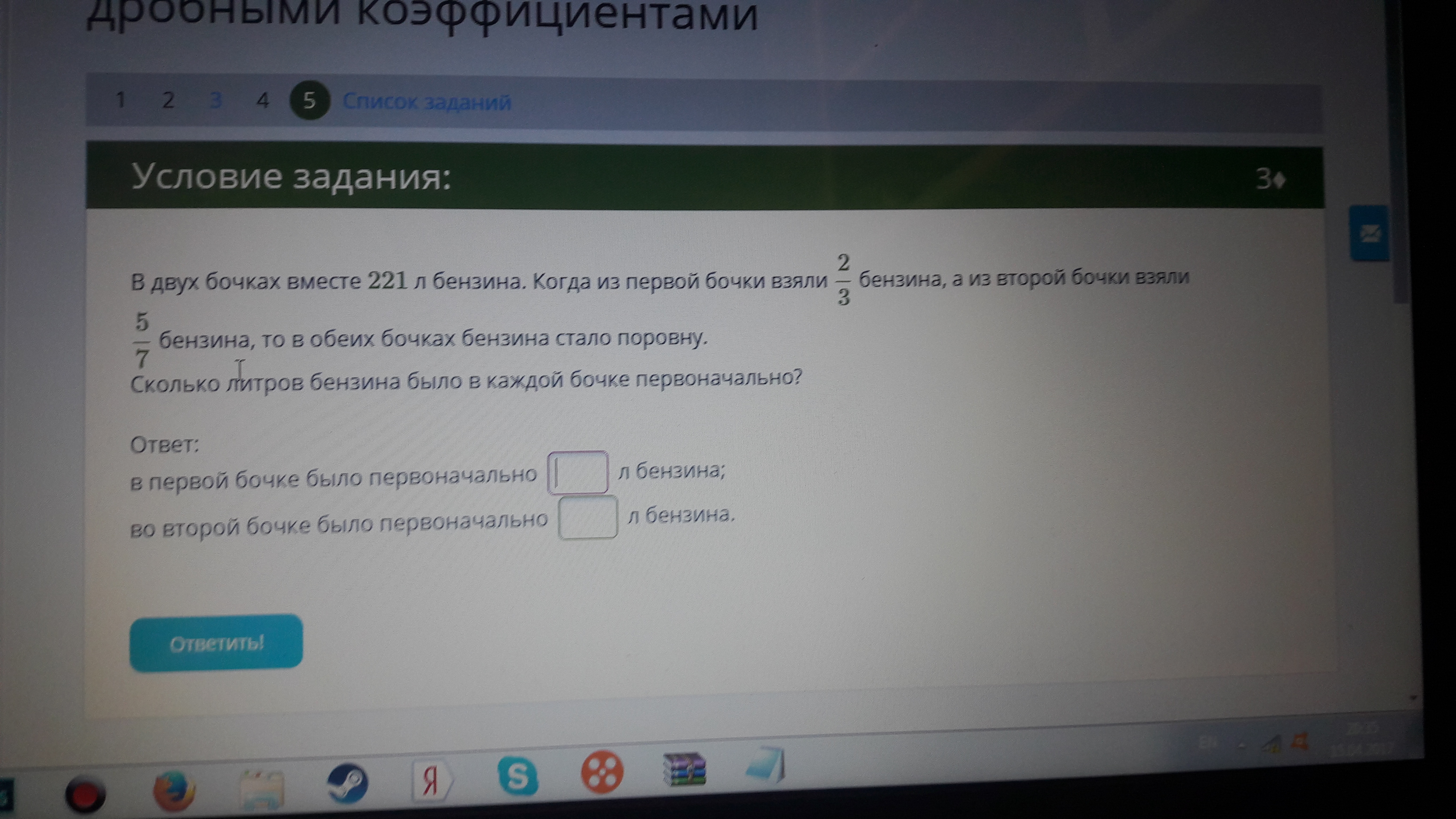
В двух бочках вместе 221 л бензина. когда из первой бочки взяли 2 и 3 бензин, А из второй бочки взяли 5 седьмых бензином, то в обеих бочках бензина стало поровну. Сколько литров бензина было в каждой бочке первоначально?

Answer 1

в первой было х ( л ) ; во второй y литров 
Cистема уравнений 
x + y = 221 
x - (2/3x )= y - (5/7y ) 
Решение 
1/3x = 2/7y 
x = 221 - y 
1/3( 221 - y ) = 2/7y 
221/3 - ( 1/3y ) = 2/7y 
221/3 = 2/7y + ( 1/3y ) 
221*7/ 21 = ( 6y + 7y ) / 21 
13y = 1547 
y = 119 ( л ) было во второй 
221 - 119 = 102 ( л ) было в первой 
Ответ 102 л ; 119 л