Предмет: Математика,
автор: Zajhgawr
Исследовать функцию с помощью первой и второй производных.
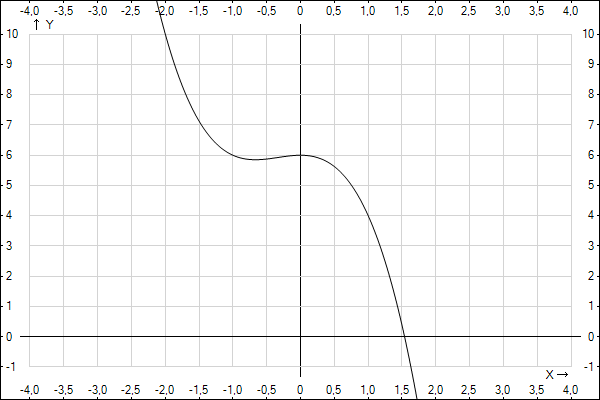
f(x)=6-x^2-x^3
Построить график.
Приложения:

Ответы
Автор ответа:
0
Рассмотрим первую производную
она имеет два корня:
между корнями производная положительна - функция возрастает, вне этого отрезка производная отрицательна - функция убывает...
Теперь рассмотрим вторую производную:
она обращается в 0 в одной точке (точка перегиба)
График функции во вложении
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: nsnsmsns
Предмет: Қазақ тiлi,
автор: urazbaevramazan157
Предмет: Информатика,
автор: dariah01042008
Предмет: География,
автор: superrstar